
数学月間の会SGKのURLは,https://sgk2005.org/ になりました.


数学月間の会SGKのURLは,https://sgk2005.org/ になりました.
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 [2017.04.11] No.162
<<数学と社会の架け橋=数学月間>>
━━━━━━━━━━━━━━━━━━━━
桜が満開で,良い季節になりましたが,大変なことばかりがどんどん起きて,平気で過ぎ去っていきます.
今村復興大臣などあきれたもの.そんな大臣がぞろぞろ居ります.防衛大臣も,法務大臣も.
第一,首相自体が問題だらけで,展望のない状態だ.それなのに,NHKの世論調査(4/7~9に実施)によると,
内閣支持53%,不支持27%という.相変わらず信じられない数字だ.
今回の調査から,現状にあわせて固定電話だけでなく携帯も含めて,RDDを行ったそうで,
(私事ながら,固定電話を3月末で廃止しました)
2,219人に調査し,1,233人から回答を得た(回答率55.6%)という.
内閣支持の理由の選択肢が,相も変わらず,「ほかの内閣よりよさそう」,「実行力がある」,...云々.
これらは,死因は「心不全」というのと同じで,理由になっていない.
結局,調査項目間の因果関係を無視した矛盾した結論言いぱなしの調査になる.
答えようのない選択肢を並べられても回答に窮する.回答率が55.6%ということがそれを物語っているのではないか.
限定条件をつけなければ答えられないところだが,単純に反応した回答だけがサンプルに拾い上げられる.
これでは偏ったサンプルが集まっていると思える.
理由を明確にするには,具体的な施策・事実を列挙しておいて,その賛否を問うべきだと思う.
ーーーーーーーーーーーーーーーーーーーー
■ステレオ投影
球面を平面に写像する方法の一つが,ステレオ投影です.球表面を平面に写像したとき,
面積,角度の両方を保存することは不可能です.ステレオ投影は,角度を保存するので,
”等角写像”です.ただし,投影円の中心付近の面積に比べて中心から離れた周囲では面積が小さくなります.
このような地図を,きっと見たことがあるでしょう.地図の他に,
多面体の面や,多面体の対称要素の配置の記述などに,ステレオ投影は欠くことができません.
さらに,双曲幾何のポアンカレの円盤モデルの理解のために,ステレオ投影は必要です.
今回は,ステレオ投影の作り方だけ,簡単に説明します.
https://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/585160/76/17100276/img_6_m?1491828971
球の北極Nに視点をおき,球面上の点を南極Sでの接平面上に投影します.例えば,P→P'
赤道(青の大円)の投影像は基円.南半球の球面上の点は基円の内部に,
北半球の球面上の点は基円の外側に投影されます.
(注)投影面を赤道を含む面として,北半球の球面上の点は南極と結び,
南半球の球面上の点は北極と結び投影する流儀もあります.
■写像の性質
この写像は等角写像なので,円は円に写像されます.
(球面)⇔(平面)
大円 ⇔ 基円上の直径両端を通る円弧
小円 ⇔ 小円
等角写像なので角度は保存され,例えば,赤道に直交する小円(南半球球面上の部分,赤点線)は,
基円に直交する円(赤の円弧)に写像されます.
■反転の利用
反転の性質を使うと,パップスの定理の様な難しいものを簡単に証明できます.
このような図形はアルベロス
(靴屋のナイフ)といいます.
この中に面白い幾何学があります.
円弧αと円弧βに挟まれたア
ルベロスの領域に,互いに接す
るように円のチェーンω0, ω1,
ω2, … があるとき, 円ωnの
中心と直径ABとの距離は円ωn
の直径のn倍である.
(パップスの定理)
[以下の証明ができます]
円ω2の中心は,線分ABから円ω2の直径の2倍だけ離れていること.
① 点Aから円ω2へ接線を引く.両接点を通りAを中心とする円γは,円ω2
と直交します.(なぜなら,円の接線は接点での半径と直交するから)
② γを反転円にして,色々なものを反転してみましょう.
円ω2 は自分自身に.円α,β は,それぞれ 直線α’,β’に,
円ω1,ω0 は,それぞれ円ω1’,ω0’に,なります.
③ 円ω2,ω1’, ω0’の直径はすべて同じだから,パップスの定理が証明
された. (なぜなら,平行な直線α‘とβ’に挟まれているから)
■円による反転鏡映の性質
①反転円の円周上の点は,反転しても元の点と同じ位置.
②反転では,円は円に変換される(直線も半径∞の円の仲間)
下図に反転円(赤い円)による,反転鏡映の例を示します.
●図1・反転円Oと交差する円Cは,交差の2点を共有する円cに変換される.
●図2・反転円Oと直交する円Cは,自分の上に変換される.
円周に直交するような反転円で分断された円の2つの部分は,反転円によるそれ
ぞれの鏡像になる.
●図3・反転円Oの中心を通る円Aは,直線aに変換される.
特に,円Bが反転円Oと交差する場合は,交差する2点をよぎる直線bに変換される.
③反転円が直線なら,普通の鏡映像になります.
直線鏡の組み合わせで作られる映像は,良く知られた万華鏡です.
反転円を用いたアポロニウスの窓も拡張された万華鏡の映像と言えるでしょう.
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 [2017.04.03] No.161
<<数学と社会の架け橋=数学月間>>
━━━━━━━━━━━━━━━━━━━━
東京ジャーミイの玄関ホールの陳列棚に飾ってある美しい皿です.直径30cm程度です.
https://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/585013/91/17866691/img_0_m?1491141557
中心の花の周りに小さい花が6個配置され,中心に6回回転対称があります.
中心(花弁12枚)の大きな花の内部は12回対称[中心にある6回対称の絵は無視します]ですが,全域的には6回対称,周囲の6個の小さな花(花弁9枚)の内部は9回対称[中心にある5回対称の絵は無視します]ですが,全域的には3回対称です.
6回対称軸と6回対称軸の間,3回対称軸と3回対称軸の間には2回対称軸が生じます.
その他,図に実線で描いたように鏡映面があります.
https://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/585013/91/17866691/img_2_m?1491141557
右側の図で水色に塗った部分が単位胞です.
この繰り返し模様は平面群P6mmの対称性で,この皿はこの繰り返し模様から,オレンジ色の円の内部だけを切り取ったものと解釈できます.
■それぞれの花の内部の局所的な対称性に言及しましょう.
中心の花の内部は,12回対称(その部分群としての6回対称は全域で通用),
周りの6個の花の内部は,それぞれ9回対称(その部分群としての3回対称は全域で通用)です.
繰り返し模様全域を支配する対称性で,12回対称や9回対称はあり得ませんので,
このような高い対称性が通用するのはそれぞれの花の内部だけですので,
あたかも,高次元宇宙からいろいろな宇宙の断面が2次元の皿の表面に投影されているようで,
不思議な魅力を感じます.
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 [2017.03.26] No.160a
<<数学と社会の架け橋=数学月間>>
━━━━━━━━━━━━━━━━━━━━
本日配信した160号の図が2つとも開かないようです.失礼しました.
本文の部分だけ,再度発行いたします.本文はこちらをご覧ください.
*****************
このグラスのデザインは,こちら側の模様の円が凹レンズとして働き,
向こう側の模様の円を円内に縮小して映し出すので,アポロニウスの窓を思わせます.
(リュミナルク製グラス)
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/566714/34/17969934/img_0_m?1490653362
■アポロニウスの窓(円の中に円を詰め込んだフラクタル)
アポロニウス(ユークリッドと並ぶ紀元前3世紀のギリシャの幾何学者)は,
3つの互いに接する円があるとき,これらの3つの円に接する円が2つ存在することを発見しました.
互いに接する3つの円(そのうちの1つが,他の2円を内部に含む外周円の場合もある)に,
接するような円の作図を繰り返して,外周円の中に円を詰め込みフラクタル構造ができます.
これをアポロニウスの窓といいます.
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/566714/34/17969934/img_1_m?1490653362
■インドラの真珠とアポロニウスの窓
仏教では,「宇宙のすべてのものが,それぞれのものの原因になっていて,
どの一人にも,無限の過去からの無数の原因が反映されている」と考えます.
これはまさに複雑系の考え方です.
宮澤賢治の小品「インドラの網」は,宇宙に張りめぐらされたインドラの網目に置かれた珠玉が,
互いに映じ合い,かつ,自分自身も輝いているさまです.
インドラの網に置かれた真珠が互いに映じ合う光景を思い浮かべましょう.
自分自身に映り込む他の真珠の映像には,もちろん自分自身も映り込み,
さらにその自分の映像中にも世界全体が.....
球の中に球を詰め込みできる美しいフラクタル図形が,”インドラの真珠”(注)です.
この美しい図形は2次元では,「アポロニウスの窓」とも呼ばれます.
(注)”インドラの真珠”,D.マンフォード, C.シリーズ, D.ライト, 小森洋平 (翻訳),日本評論社
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 [2017.03.28] No.160
<<数学と社会の架け橋=数学月間>>
━━━━━━━━━━━━━━━━━━━━
もうすぐ桜の花見ですね.こちらでは,だいぶ咲いているようですが,ときどき寒い日が戻ってきます.
どうぞお体にお気をつけください.
私の所の固定電話は,RDDの世論調査のためにあるようなもの(実際にかかって来たことはない),
あとは,オレオレ詐欺(これもかかって来たことはない)と宣伝が来るだけなので,
高額な光回線とともに本日廃止をしました.
実際に使っているのは,携帯とWiMAXです.
昨年の,数学月間懇話会では世論調査を取り上げましたが,固定電話だけから抽出するRDD方式では
サンプルの偏りが生じるのは当然でしょう.安倍内閣の驚くべき支持率の高さも現実とはかけ離れているようです.
■はじめに,お知らせですーーーーー
数学と社会の架け橋=数学月間(7/22~8/22)
数学月間懇話会は,毎年数学月間の初日7/22に実施しています.
ことしの7/22は,土曜日です.7/22が土曜日になる確率は1/7です.
365/7(mod7)=1ですから,毎年,曜日は1つづつずれます(去年は金曜日でした).
(注)ただし,うるう年は考慮していません.
ことしは,幸運にも土曜日になりました(来年は,日曜日).
例年ならお仕事などで参加できない方もどうぞお出かけ下さい.
ーーーーーー記ーーーーー
数学月間懇話会(第13回)
7月22日(土),13:50-17:20,開場:13;30
東京大学(駒場),数理科学研究科棟002号室
参加費無料,直接会場にお出で下さい.
プログラム
1.視聴率調査の実際,森本栄一(ビデオリサーチ)
2.ブラックホールを見る,池田思朗(統数研)
3.星型正多面体の体積比較(模型も作るよ!),小梁修(osa工房)
(演題は仮題です)
17:30から,学内のイタリアントマトで懇親会をします(飲食は各人払い)
ーーーーーーーーーーーー
■これから,アポロニウスの窓(あるいは,インドラの真珠)について,3回に分けて取り上げようと思っています.
このグラスのデザインは,こちら側の模様の円が凹レンズとして働き,
向こう側の模様の円を円内に縮小して映し出すので,アポロニウスの窓を思わせます.
(リュミナルク製グラス)
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/572283/34/17969934/img_0_m?1490618044
■アポロニウスの窓(円の中に円を詰め込んだフラクタル)
アポロニウス(ユークリッドと並ぶ紀元前3世紀のギリシャの幾何学者)は,
3つの互いに接する円があるとき,これらの3つの円に接する円が2つ存在することを発見しました.
互いに接する3つの円(そのうちの1つが,他の2円を内部に含む外周円の場合もある)に,
接するような円の作図を繰り返して,外周円の中に円を詰め込みフラクタル構造ができます.
これをアポロニウスの窓といいます.
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/572283/34/17969934/img_1_m?1490618044
■インドラの真珠とアポロニウスの窓
仏教では,「宇宙のすべてのものが,それぞれのものの原因になっていて,どの一人にも,
無限の過去からの無数の原因が反映されている」と考えます.これはまさに複雑系の考え方です.
宮澤賢治の小品「インドラの網」は,宇宙に張りめぐらされたインドラの網目に置かれた珠玉が,
互いに映じ合い,かつ,自分自身も輝いているさまです.
インドラの網に置かれた真珠が互いに映じ合う光景を想像ください.
自分自身に映り込む他の真珠の映像には,もちろん自分自身も映り込み,さらにその自分の映像中にも世界全体が.....
「球の中に球を詰め込む」とできる美しいフラクタル図形が,”インドラの真珠”(注)です.
この美しい図形は2次元では,「アポロニウスの窓」とも呼ばれます.
(注)”インドラの真珠”,D.マンフォード, C.シリーズ, D.ライト, 小森洋平 (翻訳),日本評論社
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 [2017.03.21] No.159
<<数学と社会の架け橋=数学月間>>
━━━━━━━━━━━━━━━━━━━━
ダ・ビンチの星型のうち,星型小12面体の話をしました.
これは,庭園美術館,朝香宮邸,姫宮の部屋の照明に使われている星型です.
もうすこし詳しく星型について,取り上げます.
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/566714/02/17957102/img_0_m?1489885670
左の図は五芒星で星型多角形,右の図は正5角形で凸多角形です.
左の星型は5/2角形,右の正多角形は5角形と記されますが何故でしょうか.
頂点Aから出発して,五芒星の辺をたどるとA→C→E→B→D→A,
星型が閉じるまでに,辺の向きが2回転します.
つまり五芒星では,1つの頂点での辺の向きの回転角は,2×360°/5 です.
比較のために,正五角形の場合は,1つの頂点で360°/5だけ回転することを思い出しましょう.
この星型多角形を5/2と書くのは,2x360°/5=360°/(5/2)だからです.
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/566714/02/17957102/img_1_m?1489885670
この星型多角形が頂点で5つづつ集まる{5/2,5}は,星型小12面体になります.
この星型は正12面体をコア(芯)にして,各正5角形の面の上に正5角錐が乗った形です.
星型の頂点は12個あり,正12面体の面に対応しますから,12個の頂点を結んでできる正多面体は
正12面体に双対な正20面体です.
■さて,この星型小12面体{5/2,5}は,プラトンの正多面体(正12面体)を芯にして,
その正5角形の面に正5角錐を貼りつけた形でした.
同様に,プラトンの正多面体(正20面体:正12面体に双対)を芯にして,
その正3角形の面に正3角錘(正4面体)を貼り付けてできる形は,星型大12面体{5/2,3}と呼ばれます.
これら2つの星型は,ケプラーの星型多面体とも呼ばれます.
序に,この2つの星型に双対な,{5,5/2},{3,5/2}はポアソンの星型と呼ばれます.
■星型小12面体は,五芒星の面Fが12枚,稜の数Eが30,頂点の数Vが12ですので,
F-E+V=-6(我々の知っているオイラーの多面体定理では2となるべき)となります.
これは星型小12面体の空間が,球の位相と異なり,穴が4つ空いた浮袋と同じ位相であるためです.
■星型正5角形の頂点Aから始めて,A→C→E→B→D→Aと辺をたどり元に戻ると,1つの頂点で2×360°/5だけ辺が回転することがわかります.
この星型5角形を5/2と書くのは,2x360°/5=360°/(5/2)だからです.
この星型5角形が頂点で5つづつ集まる{5/2,5}は,星型小12面体になります.
イメージ 1
イメージ 2
■さて,この星型小12面体{5/2,5}は,プラトンの正多面体(正12面体)を芯にして,その正5角形の面に正5角錐を貼りつけた形です.
同様に,プラトンの正多面体(正20面体:正12面体に双対)を芯にして,その正3角形の面に正3角錘(正4面体)を貼り付けてできる形は,星型大12面体{5/2,3}と呼ばれます.これら2つの星型は,ケプラーの星型多面体とも呼ばれます.
序に,この2つの星型に双対な,{5,5/2},{3,5/2}はポアソンの星型と呼ばれます.
■星型小12面体は,五芒星の面Fが12枚,稜の数Eが30,頂点の数Vが12ですので,
F-E+V=-6(我々の知っているオイラーの多面体定理では2)となります.これは星型小12面体の空間が,球の位相と異なり,穴が4つ空いた浮輪と同じ位相であるためです.
➡星型正多面体
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 [2017.03.14] No.158
<<数学と社会の架け橋=数学月間>>
━━━━━━━━━━━━━━━━━━━━
マンデルブロ(仏の数学者)は,「フラクタル」という概念の創始者(1975)です.
私たちは,ニュートンの微積分の発明以来,至る所で接線の引ける曲線を扱っていました.
フラクタル曲線というのは,これらと全く異なる曲線で,以下の性質があります.
・曲線のどんな小さな部分を拡大しても,自分全体と同じ形が現れる曲線.
・至る所ギザギザで接線が引けない曲線.
■マンデルブロ集合というのは,ちょっと変わったフラクタルです.
複素平面上で,次の漸化式を定義します.
Z(n+1)={Z(n)}^2+c, Z(0)=0
Z(n)やcは複素数で,cは定数,Z(0)は初期値といいます.
複素平面上の点cに対して,数列 Z(0),Z(1),Z(2),・・・・,Z(n),・・・ を計算していきます.
n→∞ のとき,|Z(n)|→∞ にならない(発散しない)ような
複素数cの全体が作る集合(図の黒い部分)が,マンデルブロ集合です.
面白い形をしていますが,拡大しても拡大しても(解像度を上げても)同じ構造が見えるフラクタル性があります.
(注)ある定数cに対して,数列が発散しない初期値Z(0)の集合を充填ジュリア集合といいます.
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/568618/22/17112522/img_1_m?1487235969
発散しないということは,有限な値に収束するか,有限な範囲に振動するかです.
例えば,c=-1とすると,Z(0)=0,Z(1)=-1,Z(2)=0,Z(3)=-1,・・・・は振動です.
c=-1+iとすると,Z(0)=0,Z(1)=-1+i,Z(2)=-1-i,Z(3)=-1+3i,Z(4)=-9-5i,・・・・,これは発散です.
発散しなかったc=-1はマンデルブロ集合に入り,発散したc=-1+iはマンデルブロ集合に入りません.
このようにして複素平面を塗り分けて,奇妙な形のマンデルブロ集合が出来上がります.
しかしながら,この判別が難しい,始めのうちは有限に見えたものが,nが大きくなると発散するかもしれません.
しかし,際限なく計算するわけにはいきません.現実的な判定は近似j的で,例えば,n=200まで計算して,
ある閾値を越えなければ,発散しないと判定するわけです.
そして,マンデルブロ集合(黒い部分)の協会部分は発散するのですが,
発散のスピードにより着色してみます.抽象芸術のような不思議なパターンをご覧になったことがあるでしょう.
これは,c のわずかな差により,運命が劇的に変わるカオスと秩序が入り混じってフラクタルになっている世界です.
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/568618/22/17112522/img_0_m?1487235969
マンデルブロ集合をネット上でonlineで描かせるサイトが色々あります.
例えば,http://mandelbrot.ovh.org/ などを使ってみると面白いと思います.
(注)ここで載せた参照リンク先は,現在なくなっています.マンデルブロ集合の描画は,例えば, http://e-mandelbrot.com/ などで試すことができます.
マンデルブロ(仏の数学者)は,「フラクタル」という概念の創始者(1975)です.私たちは,ニュートンの微積分の発明以来,至る所で接線の引ける曲線を扱っていました.フラクタル曲線というのは,これらと全く異なる曲線で,以下の性質があります.
・曲線のどんな小さな部分を拡大しても,自分全体と同じ形が現れる曲線.
・至る所ギザギザで接線が引けない曲線.
■マンデルブロ集合というのは,ちょっと変わったフラクタルです.
複素平面上で,次の漸化式で定義される数列を考えます.
Z(n+1)={Z(n)}^2+c, Z(0)=0
Z(n)やcは複素数で,cは定数,Z(0)は初期値といいます.
複素平面上の点cに対して,数列 Z(0),Z(1),Z(2),・・・・,Z(n),・・・ を計算していきます.n→∞ のとき,|Z(n)|→∞ にならない(発散しない)数列が作れる複素数cの全体が作る集合(図の黒い部分)が,マンデルブロ集合です.
面白い形をしていますが,拡大しても拡大しても(解像度を上げても)同じ構造が見えるフラクタル性があります.
(注)ある定数cに対して,数列が発散しない初期値Z(0)の集合を充填ジュリア集合といいます.
http://mandelbrot.ovh.org/image.php?antialias=on&func=1&a=4&x1=-2&point=on&y1=1&x2=1&y2=-1&repeats=100&xZ0=0&yZ0=0&r=2&gen=1
発散しないということは,有限な値に収束するか,有限な範囲に振動するかです.
例えば,c=-1とすると,Z(0)=0,Z(1)=-1,Z(2)=0,Z(3)=-1,・・・・と数列は振動します.c=-1+iとすると,Z(0)=0,Z(1)=-1+i,Z(2)=-1-i,Z(3)=-1+3i,Z(4)=-9-5i,・・・・,この数列は発散です.発散しなかったc=-1はマンデルブロ集合に入り,発散したc=-1+iはマンデルブロ集合に入りません.このようにして複素平面を塗り分けて,奇妙な形のマンデルブロ集合が出来上がります.
しかしながら,実際はこの判別が難しい.始めのうちは有限に見えたものが,nが大きくなると突然発散するかもしれません.現実には際限なく計算するわけにはいきませんので,判定は近似j的で,例えば,n=200まで計算して,ある閾値を越えなければ,発散しないと判定するわけです.
そして,マンデルブロ集合(黒い部分)の境界外は発散するのですが,発散のスピードにより着色しています.このような抽象芸術のような不思議なパターンをご覧になったことがあるでしょう.これは,c のわずかな差により,運命が劇的に変わるカオスと秩序が入り混じってフラクタルになっている世界です.
http://mandelbrot.ovh.org/image.php?antialias=1&func=1&a=4&x1=-1.15625&y1=0.25&x2=-0.40625&y2=-0.25&repeats=100&xZ0=0&yZ0=0&r=2&gen=1
.
マンデルブロ集合をネット上でonlineで描かせるサイトが色々あります.
例えば,http://mandelbrot.ovh.org/ などを使ってみると面白いと思います.
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 [2017.03.07] No.157
<<数学と社会の架け橋=数学月間>>
━━━━━━━━━━━━━━━━━━━━
桜もずいぶん早く咲いているのを見かけますね.皆様のところでは如何でしょうか.
今回もダ・ビンチの星型を取り上げますが,「星型小12面体」とも呼ばれる形を見てみましょう.
イメージ 1
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/572283/10/17940010/img_0_m?1488810835
シュレフリの記号で書くと{5/2,5}です.
(注)シュレフリの記号{p,q}というのは,
正p角形の面が,頂点でq個集まっているような正多面体を表す記号でした.
この形は,東京都庭園美術館,朝香宮邸,姫宮の部屋の照明器具にも使われている美しい形です.
芯になるのは正5角12面体で,その12個の正5角形の面の上に,それぞれ正5角錘を取り付けた形をしています.
正5角錐の頂点は,それぞれ,正12面体の面に対応していますから,
頂点を結んでできる図形(赤の多面体)は,正12面体に双対な正20面体です.
2次元の断面を見ると,以下の左図の様な星型正多角形(ダビデの星)が見えます.
イメージ 2
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/572283/10/17940010/img_1_m?1488810835
上図の図形は,星型5角形(ダビデの星)と星型8角形(ダ・ビンチの星型)です.
それぞれの図にある赤い輪郭線(それぞれ正5角形と正8角形)は,
凸多角形(凹所のない多角形)で,赤い輪郭線の多角形内部に,黒い線分で描いた図形が星型です.
左のダビデの星を見て下さい.
星型正5角形の辺をA→B→C→・・・→Aと1周りたどると,
辺の向き(→)が2回転することがわかります.(あるいは,
「5角形の頂点を1つ飛ばしで辿って,2周して始めの頂点に戻る」
ということもできます)
このような星形を{5/2}と表記します.
(もし,1点の周りが2x360°という世界があれば,この星型は凸多角形になります)
星型8角形でも同様で,この図形は{8/3}です.
■さて,星型正多面体を見て下さい,正5角錐の頂点の周りに,星型正多角形{5/2}が,
5個集まっていることがわかるでしょう.
従って,この星型正多面体をシュレフリの記号で書くと{5/2,5}となります.
このダ・ビンチの星型は,「星型小12面体」とも呼ばれます.
イメージ 1
シュレーフリの記号で書くと{5/2,5}です.
(注)シュレフリの記号{p,q}というのは,正p角形の面が,頂点でq個集まっているような正多面体を表す記号でした.
この形は,東京都庭園美術館,朝香宮邸,姫宮の部屋の照明器具にも使われている美しい形です.芯になるのは正12面体で,その12個の正5角形の面の上に,それぞれ正5角錘を取り付けた形をしています.正5角錐の頂点は,それぞれ,芯となる正12面体の面に対応していますから,頂点を結んでできる図形(赤の多面体)は,正12面体に双対な正20面体です.
この星型多面体の面は,以下の左図の様な星型正多角形(五芒星)です.
イメージ 2
Fig. 星型5角形(五芒星)と星型8角形(ダ・ビンチの星型)
それぞれの図の赤い輪郭線(それぞれ正5角形と正8角形)は,
凸多角形(凹所のない多角形)で,赤い凸多角形内部に星型が作図されています.
■五芒星(図左)
星型正5角形の辺をA→C→E→B→D→Aと1周りたどると,
辺の向き(→)が2回転することがわかります.あるいは,
「5角形の頂点を1つ飛ばしで辿って,2周りすると始めの頂点に戻る」
ということもできます.
このような星形を{5/2}と表記します.
(もし,1点の周りが2x360°という世界があれば,この星型は凸多角形になります)
凸多角形では,1周すると辺の向きは360°回転し,正n角形では,頂点で360°/nずつ回ります.従って,正n角形の頂角(内角)は180°-360°/nです.五芒星の頂角は36°で,正n角形の頂角が36になるのはn=5/2ですから,五芒星を{5/2}と表記するのは妥当でしょう.
星型8角形でも同様で,この図形は{8/3}です.
■さて,星型正多面体に戻りましょう.正5角錐の頂点の周りに,星型正多角形{5/2}が,5個集まっていることがわかるでしょう(例えば,頂点Aの周りに右図のような五芒星の板を5枚集める).芯に正5角形の穴の開いた五芒星の板を,各頂点で5枚ずつ組み合わせると,この立体を作ることができます.
従って,この星型正多面体をシュレーフリの記号で書くと{5/2,5}となります.
イメージ 3
デザルグの定理とは
「⊿ABCと⊿A'B'C'があり,AA',BB',CC'を通る直線が1点Oで交わるなら.
直線ABとA'B'の交点P,直線BCとB'C'の交点Q,直線CAとC'A'の交点Rは,同一直線上にある」
このデザルグの定理の証明は,実はとても難しいのです.3角形を直線が過る図形で生じる長さの比率に関するメネラウスの定理などを使う必要があります.
ところが,下図のように,この図形を平面(2次元)と見ずに,立体(3次元)にあると見ると,ごく当たり前のことを言っていることに気づきます.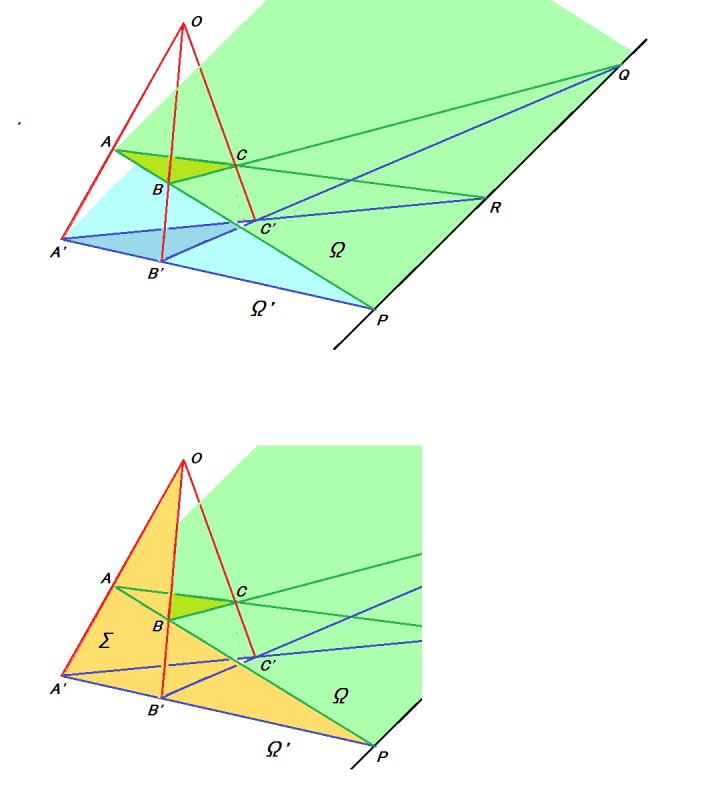
光源Oから出る光が,△ABCの影を△A'B'C'に作っています(辺ABの影が辺A'B').
従って,O,A,B,A',B' は,同一平面上にあり,この平面をΣ(薄燈)と名付けます.A,Bを通る直線も,A',B'を通る直線もこの平面Σ上にあり,P点で交差します.
一方,A,B,Pは平面Ω上に,A',B',Pは平面Ω’上にあります.
結局,P点は平面Ωと平面Ω’の交線上にあることになります.
同様にして,QもRも,平面Ωと平面Ω’の交線上にあり,デザルグの定理が証明できました.
■デザルグの定理は,2次元で証明するのは難しいが,3次元では証明が要らないほど自明なのは何故でしょうか.
3次元でこの図のような模型があったとして,これを2次元に射影する(高さ方向をぺちゃんこ)と,直線が交差する状況は変わらないのですが,長さや角度の情報が失われてしまいます.△ABCと△A'B'C'は,それぞれ別の2次元平面にあったものですが,ぺちゃんこにされて1つの平面(紙面)に入ってしまいました.
私たちは,高い次元(2次元の世界から3次元の世界)を想像するのは困難です.デザルグの定理でこれを思い知らされます.
■デザルグは,17世紀初頭のフランスの数学者,建築家.透視図法を発展させた射影幾何学の祖です.ダビンチなどの画家たちは,遠近法や透視図法を古くから用いていましたが,その数学を固め射影幾何学の本を出したのはデザルグが最初です.
その後,射影幾何学が本格的に研究されるのは,200年後の19世紀中葉,ポンスレー(フランスの数学者.ナポレオンのロシア遠征に従軍し,ロシアで捕虜のときに射影幾何学を研究した)を待たねばなりませんでした.
射影幾何学自体,作図など重要な応用がありますが,やはり,19世紀中葉に現れた非ユークリッド幾何学のモデルを作るための重要なツールとなりました.
デザルグの定理とは
「⊿ABCと⊿A'B'C'があり,AA',BB',CC'を通る直線が1点Oで交わるなら.
直線ABとA'B'の交点P,直線BCとB'C'の交点Q,直線CAとC'A'の交点Rは,同一直線上にある」
このデザルグの定理の証明は,実はとても難しいのです.3角形を直線が過る図形で生じる長さの比率に関するメネラウスの定理などを使う必要があります.
ところが,下図のように,この図形を平面(2次元)と見ずに,立体(3次元)にあると見ると,ごく当たり前のことを言っていることに気づきます.
イメージ 2
2つの平面Ω(薄緑)とΩ’(薄青)が交差しており,△ABCは平面Ω上に,△A'B'C'は平面Ω'上にあります.
光源Oから出る光が,△ABCの影を△A'B'C'に作っています(辺ABの影が辺A'B').
従って,O,A,B,A',B' は,同一平面上にあり,この平面をΣ(薄燈)と名付けます.A,Bを通る直線も,A',B'を通る直線もこの平面Σ上にあり,P点で交差します.
一方,A,B,Pは平面Ω上に,A',B',Pは平面Ω’上にあります.
結局,P点は平面Ωと平面Ω’の交線上にあることになります.
同様にして,QもRも,平面Ωと平面Ω’の交線上にあり,デザルグの定理が証明できました.
■デザルグの定理は,2次元で証明するのは難しいが,3次元では証明が要らないほど自明なのは何故でしょうか.
3次元でこの図のような模型があったとして,これを2次元に射影する(高さ方向をぺちゃんこ)と,直線が交差する状況は変わらないのですが,長さや角度の情報が失われてしまいます.△ABCと△A'B'C'は,それぞれ別の2次元平面にあったものですが,ぺちゃんこにされて1つの平面(紙面)に入ってしまいました.
私たちは,高い次元(2次元の世界から3次元の世界)を想像するのは困難です.デザルグの定理でこれを思い知らされます.
■デザルグは,17世紀初頭のフランスの数学者,建築家.透視図法を発展させた射影幾何学の祖です.ダビンチなどの画家たちは,遠近法や透視図法を古くから用いていましたが,その数学を固め射影幾何学の本を出したのはデザルグが最初です.
その後,射影幾何学が本格的に研究されるのは,200年後の19世紀中葉,ポンスレー(フランスの数学者.ナポレオンのロシア遠征に従軍し,ロシアで捕虜のときに射影幾何学を研究した)を待たねばなりませんでした.
射影幾何学自体,作図など重要な応用がありますが,やはり,19世紀中葉に現れた非ユークリッド幾何学のモデルを作るための重要なツールとなりました.
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 [2017.02.21] No.155
<<数学と社会の架け橋=数学月間>>
━━━━━━━━━━━━━━━━━━━━
■ユニット折り紙で作ったダビンチの星型の続きです.これは,
芯に置いた正8面体の各面に正3角錘が乗っている形です.Fig.4
星型の頂点を結ぶと芯にある正8面体に双対な正6面体ができます.
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/572283/19/17902919/img_0_m?1486823996
このユニット折紙では,正3角錐の面は正3角形ではなく直角3角形です.
そして,各面はツートンカラーになっています.
対称性を調べると,芯の正8面体の頂点方向に(x,y,z軸)4回回転対称軸,
各正3角形の面に垂直に3回回転対称軸,2つの4回回転軸の中間(同じことだが,2つの3回回転軸の中間)に
2回回転対称軸があります.色の変化を調べると,
4回回転軸により4色の置換,3回回転軸により3色の置換と1色の保存,
2回回転軸により2色の置換と2色の保存が起こります.
この図形には4回軸があるので,色置換の操作も含めて完全な対称性にするには,
塗り分けには4色用いる必要があります.
3回軸の方向から見ると3色見え,見えないもう一色は,
3回軸で保存され,3回軸に垂直な面の大円上にあります.
3回軸の方向は4本あり,3回軸それぞれは,軸に垂直な大円上の色を保存するので,
結局,塗り分けには全部で4色使うという言い方もあります.
■写真(Fig.5)
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/566714/18/17913418/img_0_m?1487566646
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/566714/18/17913418/img_1_m?1487566646
この星型は,立方体の6つの面に,正3角形の面で出来ている正4角錐が乗っています.
芯になる立方体の1辺の長さを1とすると,星型の頂点の高さは√2/2,
もし,星型頂点の高さを立方体の辺の長さの1/2に短縮すると,
星型の凹入角がフラットになり体心格子のデリクレ胞(菱形12面体)になります.
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/566714/18/17913418/img_4_m?1487566646
(Fig.6)左が星型正24面体,右が菱形12面体
展開図は色々なものができますが,作りやすいものにするのがよい設計です.
星型24面体と菱形12面体の展開図を比較して見て下さい.(Fig.7)
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/566714/18/17913418/img_6_m?1487566646
美しい形ですので作って見ると良いでしょう.
■正20面体を芯にして,正3角形の各面の上に正3角錘(正4面体)を乗せた星型が,星型正60面体です.
正3角形の面が10個集まっている点と3個集まっている点(頂点)が交互にある星型です.
1枚の連続した紙に展開図を描くことはできません.
写真の星型は,立方体の6つの面に,正3角形の面で出来ている正4角錐が乗っています.芯になる立方体の1辺の長さを1とすると,星型の頂点の高さは√2/2,もし,星型頂点の高さを立方体の辺の長さの1/2に短縮すると,星型の凹入角がフラットになり体心格子のデリクレ胞(菱形12面体)になります.
■星型の展開図です.
展開図はいろいろなものが考えられますが,作りやすいように設計するとよいと思います.
■星型正24面体と菱形12面体
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 [2017.02.14] No.154
<<数学と社会の架け橋=数学月間>>
━━━━━━━━━━━━━━━━━━━━
星型を作って見ました.展開図を考えて組み立てました.展開図には色々な変形があり,
紙の使用量が小さくなるようにくふうするのも面白いです.糊代に立体内部から糊付けするのはちょっと面倒でした.
■この金平糖のような形(Fig.1)はダ・ビンチの星型の一つです.芯の部分に正12面体があり,
その正5角形の12個の面の上に,正5角錘が乗っています.だから星の頂点は12個で,
12個の頂点を結んでできるのは正12面体に双対な正20面体です.一つの頂点の真上から見ると,
五芒星と五芒星の中に正5角形が見えます.五芒星の腕の長さと中にある正5角形の辺の比は黄金比です.
この星型多面体の面(2等辺3角形)は,黄金比の三角形です.
もし,面の形を正3角形にすれば,星形正60面体が得られます.どちらもダ・ビンチの橋形と言います.
特にこの写真の黄金比が出て来る方は美しいですね.
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/572283/58/17899558/img_1_m?1486673391
■プラトンの正多面体は正多角形の面で出来ている凸の正多面体で5種類あります.
プラトンの正多面体を芯にして,正多角形の各面の上に正多角錘(面は正3角形)を乗せると,
ダ・ビンチの星型ができまので,ダ・ビンチの星型も5種類できます.その作り方から自明ですが,
それぞれのダ・ビンチの星型と対応するプラトンの多面体は互いに双対です.
■例えば,正4面体の4つの面のそれぞれに正4面体を貼り付けた形(Fig.2)を見ましょう.
この星型の頂点は4つで,頂点を結ぶと,また正4面体になります.
これは,正4面体の双対図形が正4っ面体であることからわかります.
正4面体が5つ(芯にあるのは見えません)で出来ています.
これを4次元の世界で組み立てると4次元の正5胞体(5つの3次元の正4面体を面に持つ4次元の立体のこと.
4次元多面体の面は3次元の多面体)ができます.その意味で,この星型は,4次元正5胞体の3次元の展開図といえます.
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/572283/65/17901765/img_1_m?1486690977
■もう一つ例をあげれば,正8面体を芯にして,
正8面体の8つの正3角形の面にそれぞれ正4面体が乗っている形の星型(Fig.3)です.
互いに点対称にある2つの大きな正4面体が噛み合った形です.星型の頂点を結んでできる図形は,
正8面体に双対な正6面体です.
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/572283/01/17905101/img_0_m?1486868408
■次に示すユニット折り紙も,ダビンチの星型です.正8面体の各面に正3角錘が乗っています.
この折紙では,正3角錐の面は正3角形ではなく直角3角形です.そして,各面はツートンカラーになっています.
この図形には4回回転対称軸や3回回転対称軸,2回回転対称軸などがあります.
これから先はこの図形の対称性と色置換の話ですが,長くなるので次号にします.
http://blog-001.west.edge.storage-yahoo.jp/res/blog-09-2d/tanidr/folder/572283/19/17902919/img_0_m?1486823996
星型を作って見ました.展開図を考えて作り,それを組み立てました.展開図には色々な変形があり,紙の使用量を小さくするような工夫も面白いです.糊代に立体内部から糊付けするのはちょっと面倒でした.
■この金平糖のような形(Fig.1)はダ・ビンチの星型の一つです.芯の部分に正12面体があり,その正5角形の12個の面の上に,正5角錘が乗っています.だから星の頂点は12個で,12個の頂点を結んでできるのは正12面体に双対な正20面体です.一つの頂点の真上から見ると,五芒星と五芒星の中に正5角形が見えます.五芒星の腕の長さと中にある正5角形の辺の比は黄金比です.この星型多面体の面(2等辺3角形)は,黄金比の三角形です.
もし,面の形を正3角形にすれば,星型正60面体が得られます.どちらもダ・ビンチの星型と言います.特にこの写真の黄金比が出て来る方は美しいですね.
■プラトンの正多面体は正多角形の面で出来ている凸の正多面体で5種類あります.プラトンの正多面体を芯にして,正多角形の各面の上に正多角錘(面は正3角形)を乗せると,ダ・ビンチの星型ができまので,ダ・ビンチの星型も5種類できます.その作り方から自明ですが,それぞれのダ・ビンチの星型と対応するプラトンの多面体は互いに双対です.
■例えば,正4面体の4つの面のそれぞれに正4面体を貼り付けた形(Fig.2)を見ましょう.この星型の頂点は4つで,頂点を結ぶと,また正4面体になります.これは,正4面体の双対図形が正4っ面体であることからわかります.
正4面体が5つ(芯にあるのは見えません)で出来ています.これを4次元の世界で組み立てると4次元の正5胞体(5つの3次元の正4面体を面に持つ4次元の立体のこと.4次元多面体の面は3次元の多面体)ができます.その意味で,この星型は,4次元正5胞体の3次元の展開図といえます.
■もう一つ例をあげれば,正8面体を芯にして,正8面体の8つの正3角形の面にそれぞれ正4面体が乗っている形の星型(Fig.3)です.互いに点対称にある2つの大きな正4面体が噛み合った形です.星型の頂点を結んでできる図形は,正8面体に双対な正6面体です.
ーーーー
■次に示すユニット折り紙も,ダビンチの星型です.芯にある正8面体の各面に正3角錘が乗っています.この折紙では,正3角錐の面は正3角形ではなく直角3角形です.そして,各面はツートンカラーになっています.
対称性を調べると,芯の正8面体の頂点方向(x,y,z軸上にある)4回回転対称軸,体対角線の方向に3回回転対称軸,2つの4回回転軸の中間(同じことだが,2つの3回回転軸の中間)に2回回転対称軸があります.
4回回転軸により4色の置換,3回回転軸により3色の置換と1色の保存,2回回転軸により2色の置換と2色の保存が起こります.星型の頂点を結ぶと芯にある正8面体に双対な正6面体ができます.
(Fig.4)
この図形には4回軸があるので,色置換の操作も含めて完全な対称性にするには,塗り分けには4色用いる必要があります.3回軸の方向から見ると3色見えます.見えないもう一色は,3回軸で保存され,3回軸に垂直な面の大円上にあります.
立方体では,3回軸の方向が体対角線方向に4本あり,3回軸それぞれに,軸に垂直な大円が色を保存するので,結局,全部で4色使うという言い方もあります.
■写真(Fig.5)の星型は,立方体の6つの面に,正3角形の面で出来ている正4角錐が乗っています.芯になる立方体の1辺の長さを1とすると,星型の頂点の高さは√2/2,もし,星型頂点の高さを立方体の辺の長さの1/2に短縮すると,星型の凹入角がフラットになり体心格子のデリクレ胞(菱形12面体)になります.(Fig.6)
イメージ 1イメージ 2
Fig.5
■星型正24面体の展開図
イメージ 3イメージ 4
展開図はいろいろなものが考えられますが,作りやすいものを設計するとよいと思います.
■星型正24面体と菱形12面体
イメージ 5
Fig.6
星型正24面体 菱形12面体
以下に星型正24面体と菱形12面体の展開図の比較を示します.
イメージ 6
■正20面体を芯にして,正3角形の各面の上に正3角錘(正4面体)を乗せた星型が,
星型正60面体です.正3角形の面が10個集まっている点と3個集まっている点(頂点)が交互にある星型です.1枚の連続した紙に展開図を描くことはできません.
日刊ベリタ(2月3日)に掲載
■2月2日,17時からの東電会見で,福一2号機の格納容器内の映像についての報告がありました.この会見は定例で月・木に行われ,各社の記者にまじって,おしどりマコさんも必ず出席されています.私は,IWJのインタネット中継でこれを見ています.皆様もご覧になることをお勧めします.ただし,東電の説明はとても下手で,一般向けに説明しません.そこで,東電の発表事実を踏まえた上で,私の解説を加えてこの記事を書きました.
■2月2日に発表されたのは,1月30日に実施した挿入カメラによる画像を解析した結果です.この実験は24日,5:30-8:00,26日,5:45-9:10,にも実施されています.カメラは格納容器のX6ペネという導入窓に直径11cmの穴を穿孔(この穿孔も大変でした.詳細は私のブログにあります),物干し竿の先につけた固定焦点のカメラをレールに沿って移動させ挿入しました.2月に,「原子炉圧力容器」を下から支える,コンクリートの部屋(ペデスタル)の中に,自走式のサソリ型ロボットを投入して観察しようというのです.これはそのための偵察実験です.
■原子炉格納容器内で,「圧力容器(原子炉容器)」を支えているコンクリート製の構造物が「ペデスタル」.ペデスタル内に入り天井を見上げると,「圧力容器」の底から出ている多数の制御棒挿入機構や配管が配列しています(正常なら).
原子炉建屋で言うと,「原子炉圧力容器」は2,3階を占め,ペデスタルは地下から1階を占めます.「原子炉圧力容器」を包む格納容器は地階から4階を占めています.
「原子炉圧力容器」の直径は7mほど,高さは22mあり,格納容器はこれを内部に含む大きなフラスコの様な形をしています.
ペデスタルの入り口は,高さ1mほどで,屈まないと入れません.広さは直径7mほどの円形の空間で,天井には「原子炉圧力容器」の制御棒駆動機構に繋がるスタブチューブフランジが並んでいます.この配管に水圧をかけると,上にある制御棒が上昇し,燃料体に挿入される仕組みになっています.3.11の時も,制御棒の挿入まではうまく行ったということです.
■1号機,3号機は,事故当時,ウエットベントが出来ましたが,それぞれの建屋は水素爆発しました.1号機は白煙,3号機は黒煙をあげて爆発したことを記憶されていることでしょう.どちらも核燃料はメルトダウンして,ほぼすべてが溶け落ちた可能性が高いと東電も認めています(2014.8.6).続いて,2号機も2011.3.14日深夜に格納容器圧力が異常上昇するもベントに失敗,圧力抑制室が破損し,直接放射性物質をばらまきました.15日,6時10分に圧力抑制室の圧力が外気と同じ1気圧になったのです.
圧力抑制室というのは,建屋の地下にある直径33.5mのドーナツの様な形の水の入ったプールです.格納容器とはベント管というパイプ(直径2m,8本ある)で繋がっています.
■2号機では,メルトダウンした核燃料の70%~100%が圧力容器の底にたまっているらしいことは,ミュー粒子(宇宙線)を用いた透視で判明しています(2015.3).同様の透視法で1号機のメルトダウンした核燃料は圧力容器にはとんどなく,圧力容器から抜け落ちたことがわかります(IRID資料,2016.10.4).
(注)装荷核燃料の量は,1機あたり約1トンです.
特に,3号機はプルサーマルで,我々の反対を押し切り,プルトニウムを含むMOX燃料が装荷されて運転を始めたところでした.
■1月30日までの2号機での偵察実験でわかったことは以下のようなものです.
サソリ型ロボットを走行させる床(グレーチング)の一部(1m^2)に脱落しかかった場所や脱落や障害物があり,可能であるかも含めて走行ルートの検討が必要である.X6ペネから格納容器内にカメラを挿入したとき,X6の内側で50Sv/h,原子炉直下のペデスタルに達する手前の2.3mの位置で530Sv/h,ペデスタルの入り口付近では20Sv/hの線量率が観測された.東電は明言を避けていますが,格納容器内のペデスタルの外が線量率が高いというのは予想外で,デブリがペデスタルの外に落ちているのではないか.おそらくデブリは水の外に出ていて遮蔽されていないし,事故の経緯を思い出すと,デブリの一部は,格納容器も破り地下の圧力抑制室に達した可能性も考えなければいけないと私は推測します.
核燃料デブリは,高い放射能を持ちます.原子炉に核燃料が入っているから,止めていても稼働しても同じことで,使わないのは損だというような暴論を言う経済評論家が居ります.とんでもない.新しい核燃料は人がそばにいても大丈夫ですが,使用済み核燃料には,核分裂で生じた放射性の高い核種がたくさん含まれます.さらに,核分裂が起きている核燃料からは中性子がたくさん出て,周りの物質を放射化(例えば,構造物のステンレスに当たると,普通の鉄やコバルトを放射性のある同位体に変える)し,これらを含むデブリは高い放射性を持ち人が扱えません.
■今回の放射線量率の算定は,画像のノイズから(誤差が30%と大きい)ということで,東電は確定的な判断は避けています.ちょっと説明不足なので,解説を加えると,画像のノイズは,カメラの中にあるCCD(半導体)に入るγ線のためで,画像に写っている場所から来ているのではない.カメラの通った場所の線量率であります.
今後,ロボット走行のルートが確保でき投入したとしも,サソリ型ロボットの眼となるCCDの累積寿命は1,000Svなので,高い線量率の場所があると短時間で壊れてしまう恐れがあります.また,デブリが地下の圧力抑制室に達しているなら,除去は無駄
ではないかと思います.作業者の被ばく量(現在3mSv/日で管理)はさらに増加するでしょう.
「雪は天から送られた手紙(中谷宇吉郎)」という言葉がありますが,雪の結晶が生まれ・成長した気圏の状況により,様々な形の雪片が観察できます.これらの写真の中で,絶対にありえない雪の結晶が2つあります.どれとどれでしょうか?
(以下は,追補)
雪片の形の対称性は6mmです.これは雪(氷)の結晶の内部構造(分子配列)が外に反映されたものです.以下に氷の結晶構造の2次元模式図を示します.水分子はH2O(酸素原子O●の両側に水素原子H●が結合し,その結合角度は約120°)で,両端の水素原子は,隣の分子の酸素原子と弱い相互作用(水素結合)をしています.そのためこのような6mmの対称性の結晶になります.
(注)雪片(雪の結晶)の形は,デンドライトという形です.
これは,比較的速く結晶が成長するときにできます.
金平糖も似たような現象で出来るデンドライトといえますが,
1粒の金平糖全体で砂糖結晶の方位が揃った単結晶というわけでは
ないので,それが雪の結晶とは違うところです.