
数学月間の会SGKのURLは,https://sgk2005.org/ になりました.


数学月間の会SGKのURLは,https://sgk2005.org/ になりました.
1⃣ 部品一覧
2⃣ 鏡筒を組み立てる
3⃣ 鏡筒を内箱にセットする
4⃣ 内箱を外箱にセットし組み立てる
5⃣ ワンドを作る
6⃣ ブリュースターLI型万華鏡の完成
万華鏡には合わせ鏡の原理が使われています.私の前に鏡,私の後ろにも鏡,つまり,合わせ鏡の間に私が居るとします.前の鏡に写るのは,私の前から見た姿:実物の私が北向き(N)なら,鏡像は南向き(S).後ろの鏡には,私の後ろ姿の鏡像があり,これも南向き(S)です.横から,これらの像の配列を見るとSNSの配列です.
しかし,これだけで終わらないのが合わせ鏡の醍醐味です.
私の前の鏡でできた鏡像(S)は,私の後ろの鏡で反射し,後ろの鏡の中に鏡像(N)を作ります.反射するたびに像の向きは逆転しますが,生ずる像がこれで終わりということはありません.その像は,合わせ鏡のどちらかの前にありますから,次の像が必ず生じます.こうして,1列に無限に配列する鏡像の列・・・・・SNSNSNSN・・・・・ができます.これは,SNのペアが周期的に並んでいる状態です.
もし,合わせ鏡が平行ではなく,交差角 $${θ°}$$であったとすると,鏡像は直線上に並ぶのではなく,円周上に並びます.そして,SNのペアの中心角は$${2θ°}$$ですから,円周上に並んだ鏡像が周期的にきれいにつながるためには,
$${360 ^\circ /2\theta ^\circ =n}$$, $${n}$$は整数でなければなりません.
万華鏡”Kaleidoscope”の命名と発明は,ブリュースターの特許(1817年)が起源です.特許には,2枚の鏡の交差角$${θ°}$$を「360°を偶数で割り切る角にする」ことが記載されています.
ブリュースターはエディンバラの偉大な物理学者(光学)で,燈台のレンズの軽量化を実現しました.(凸レンズが大きくなると重くなるのが問題でしたがこれを解決しました.これは,その後に現れるフレネルレンズやゾーンプレートの先駆です)
また,光の反射で,反射光が完全なS偏光(反射面に平行な光電場振動成分の偏光)になる入射角に名前を残しました(ブリュースター角と呼ばれる).
今,あなたは鏡に向かい会っているとします.鏡の中には,あなたとあなたの周りの世界が写っています.あなたが実在する世界と鏡像の世界は,何から何まで同じようですが,決定的に異なるところがあります.あなたが,もし,鏡像の世界に入り込めたとしても,鏡像と重ね合わさることは決してできません.右・左が異なるからです.3次元空間でどのように動かしても,右手と左手を重ね合わせることはできません.しかし,右手と左手は鏡に映す(鏡映操作)と重ね合わすことができます.鏡映操作というのは,3次元空間内の運動ではないのです.しかし,3次元の鏡映像は,4次元空間内の運動なら重ね合わせることは可能です.
私たちは,鏡映像に何か不思議な感じを抱くのですが,鏡映像の世界には我々の3次元空間内の運動で到達できないということに関係があるのではないでしょうか.
基本的な万華鏡は,3枚鏡の壁で囲まれた3角柱でできていて,3角形の内部にガラス屑の分布した絵柄(3角形内部が非対称要素)があります.わたしは,この3角形のことを”鏡室”と呼ぶことにしています.3角形の辺の鏡映操作の従い,鏡室の絵柄を張り詰めていくと,秩序のある平面模様ができます.
秩序のある張り詰めができるためには,鏡室の3角形の形に,どのような条件が課されるでしょうか.
3角形の各頂点は合わせ鏡になっていますから,きれいに平面を3角形で埋めるには,それぞれの頂点には偶数個の3角形が集まる必要があります.この方程式を解くと,周期的に平面を埋める万華鏡パターンが得られる3角形は次の3種類に限られることがわかります.
整数解の万華鏡
分数解の万華鏡
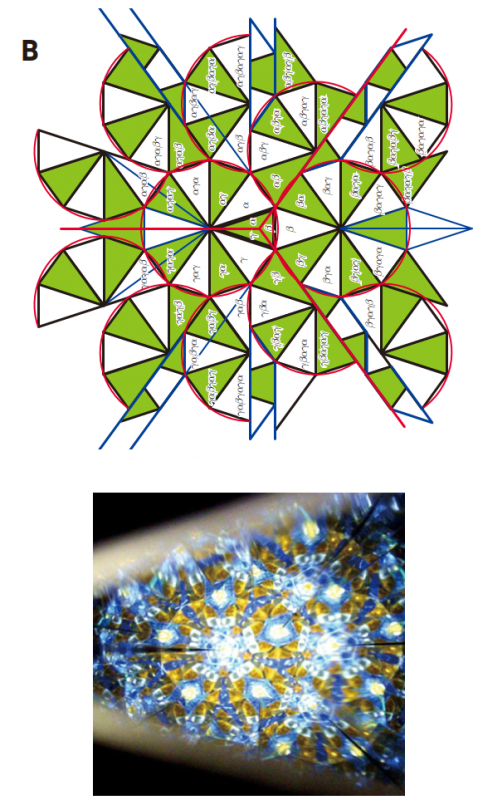
今回,なかのZEROで作る万華鏡は分数解($$ n=m=\displaystyle \frac{24}{11}$$,$$p=12 $$)82.5°・82.5°・15°の3角形です.
(引用)ここで用いた図の多くは,「美しい幾何学」,谷克彦,技術評論社(2019),第5章より引用した.
■練習問題--------------------------------------
青い正3角形が鏡室で,赤線は鏡です.鏡室を鏡で反射させると,下図のように模様が広がって行くことを確かめましょう.
このようにして,平面全体を隙間なく埋め尽くします.
*****************************************************************************************
(1)材料
(2)作り方
(3)映像
この映像が見える万華鏡の鏡室(3角形)は,頂角が15°の2等辺3角形[鏡室の各頂点での鏡の交差角は(15°,82.5°,82.5°)]で,各頂点に見える映像の回転対称性$$ (n,m,p) $$は,分数解(12,24/11,24/11)となる万華鏡です.この分数解$$ (n,m,p) $$は,確かに,$$ 1/12+11/24+11/24=1 $$なので,$$ 1/n+1/m+1/p=1 $$の条件を満たしています.
■ブリュースター型は,II鏡タイプもあります.
II鏡タイプの場合の映像は
(1)材料
鏡3枚の組み合わの違いで,セットA~Hの8種類あります.
1mm厚の光輝アルミ板(厚いので像歪みが少ない表面鏡)を,3枚組み合わせると,
所望の3角形になるよう計算して工場でカットしています.
鏡以外の部品は,セットA~Hのどれでも共通です.
ガラス屑は琉球ガラス(入手が困難になりましたので在庫限り)ですので透明度が良く奇麗です.
(注意)
⑦透明ビニール・テープ,⑧洗濯糊(PVA)は,ワークショップでは用意しますが,
材料販売では添付していません.百均ショップでお求めください.
必要な道具:はさみ(ビニール・テープを切る)
スポイド,または,ドレッシング容器など
(80%の洗濯糊[洗濯糊8:水2]をラウンドケースに滴下する)
(2)作り方
(3)サンプル映像A~G