投稿日時: 2021/01/20
 システム管理者
システム管理者
繰り返し模様の対称性の第10類は,国際記号で$$p4$$,ロシア式記号で$$(a:a):4$$.単位胞の図形の対称性$$4$$を,直交する軸(従って,正方形のメッシュが格子)に沿って並進して得られるパターンで,$$(a:a):4$$で記述される.以下の2つのエジプト模様の例は,ちょっと見るとこの対称性のようですが,厳密には,この対称性を満たしません.
問 どこがいけないのか間違い探しをしましょう.
解答
左のパターンでは,背景にストライプがありますので,4回対称軸は2回対称軸に低下します.そして,格子は直交している必要がなくなり,対称性は$$(a:a):2=(b/a):2$$になります.
右のパターンでは,コイルの渦巻きは2回回転対称のようですし,花は花弁が10枚のようですから,単位胞の中身は全体として4回回転対称になりません.
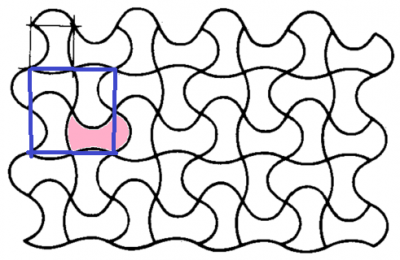
等価なパーツが隙間なく平面を充填するパターンの例
この対称性のパターンは,正方形の格子並進,4回軸がありますが,鏡映面はありません.モチーフ(非対称要素)は単位胞の1/4(例えば薄桃色)です.パターン全体を見ると,それぞれのパターンには対掌体(風車の回り方が逆なもの:chiral,enantiomorphs)が存在します.
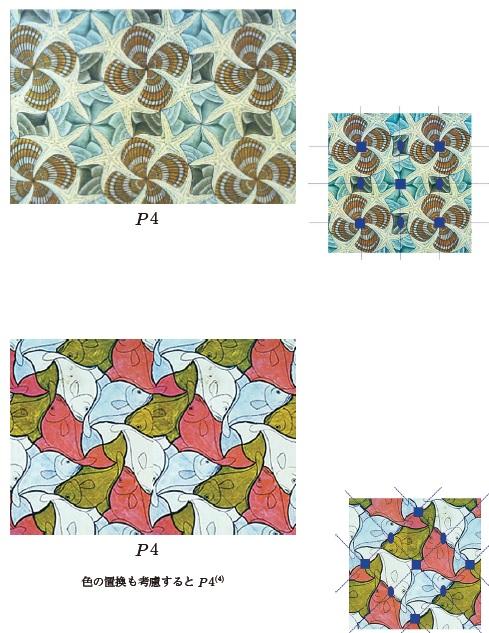
この対称性のエッシャー作品の例を以下に示します.