17種類の壁紙模様の対称性の第8類は,
国際記号で$$cmm2$$,ロシア式記号で$$(a/a):2・m$$ です.
点群$$2・m$$の図形を,並進の大きさは等しいが対称面(赤線)には斜交する軸(青線)$$(a/a)$$に沿って並進させて得られるので,$$(a/a):2・m$$と記述できる.
あるいは,面心格子$$c$$[黒いダイヤに注目すると面心格子が見えてきます]で,同じ点群$$2・m$$の図形を並進させると得られる.
菱形格子[単純格子]$$(a/a)$$の単位胞の面積は,面心格子[2格子点を含むものが単位胞]$$(c/b:a)$$の単位胞の面積の1/2です.
$$(c/b:a):2・m$$
$$(c/b:a)$$が面心格子を表し,$$m$$は赤い鏡映面を表し,鏡映面の交点には紙面に垂直に2回軸がある.
$$(a/a):2・m$$
菱形格子(単純格子)$$(a/a)$$を採用すると,このように記述できる.
これら両者の記号は同じ対称性を表現している.$$(c/b:a):2・m=(a/a):2・m$$
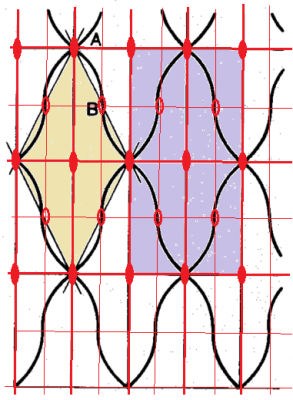
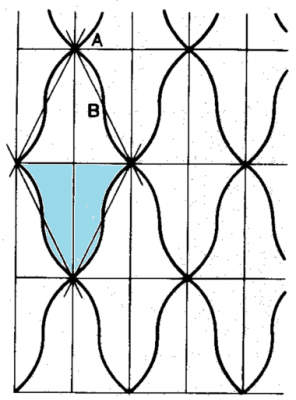
このような対称性で,等価なパーツだけで平面を隙間なく(重なることもなく)充填するパターンは次のようなものです.釣鐘の形が非対称要素(モチーフ・タイル)で菱形の単位胞(単純格子)は2つの釣鐘型からなり,面心格子の単位胞は,4つの釣鐘型からなります.
次の例は,この対称性の日本の伝統文様「菱文(ひしもん)」です.この図はネットからお借りしました.
■平面群の記号,$$(c/b:a):2・m$$や$$(a/a):2・m$$の記述に使うのは,群を定義する最小の対称要素[群の生成元]だけ記載します.下図を見てください.完成した平面群の対称要素のなかには,生成元だけでなく,細い赤い線[映進面]や白抜きの赤い2回軸が生じています.
菱形格子と,面心格子のそれぞれの単位胞を下図に着色して置きました.