10.群論の基礎.古典結晶群
これまでの章で,形而下の幾何学図形や物質形態の対称性に関する古典論の基礎を,複雑な数学ぬきで説明した.近年,対称性の研究は広汎な新領域で充実が見られ,多くの新分野に応用されている.
これらについて語るために,まず数学的知識を少しく補足し,群論の思想と表現を一貫して利用できるようにしよう.読者は最初に読む時は,この章と次の章の難しい所は,絵と例を見るだけにして飛ばしても良い.
群概念の定義.
幾何学的あるいは物理学的対象物の変換群.抽象群.
現代の数学,物理学における群概念は,数,集合,関数と言った概念と同様に,基本的な概念である.既に何度も(対称)図形の対称変換群[(有限または無限の)図形において,各部分は互いに入れ換えるが,図形全体は不変であるような対称変換の作る有限群あるいは無限群]について言及したので,部分的にではあるがそれを知っている.不変性(変換が図形の構造を保存する)の要請は,図形の対称変換群の定義の基礎となっている.
どのような図形変換を許すかにより,等長変換(isometric)群か非等長変換(nonisometric)(アフィン, 射影,トポロジ-,等)群かになる.回転群(第1種の変換),回転と鏡映の群(第2種の変換)のような直交群や,運動群(第1種と第2種の変換と並進の結合)は図形の計量特性(すべての線分の長さとそれらのなす角度)を保存する.いままでの所では,我々は変形のない(計量保存)図形変換である直交群と運動群とを扱つていた.
アフィン変換群は,無限な図形,媒質で許される一様変形(伸張,圧縮,ずり)の集合からなる.等方で一様な空間はアフィン対称である。相似変換群(アフィン変換群の特殊な場合)は植物や動物の構造や成長の対称を記述する;相似変換は建築物の細部や,遠近法に従って描いた絵画に見られる.
重要な非直交群の例は,図形の等価な部分の任意の置換である.この置換は図形を自分自身に変換する(例えば,結晶構造における同価な原子の置換全部が作る群,原子核構造における中性子の置換全部が作る群など).特殊な場合には,置換群は直交群に同型となることを後に知るであろう.
変換の概念は,幾何学的対象(有限図形,連続体,離散体)に関してだけでなく,物質図形,スカラ-,ベクトル,テンソル場のような(物理的性質を担っている形而下の)物理的対象に関しても定義できる.このような対象は,直交変換群だけでなく,次のようなさらに一般的な変換群に従う: 結晶物理や結晶の構造解析で利用する反対称群と色対称群(次の章でこれらの群を学習する);素粒子理論で使われるユニタリ-群(ユニモジュラ-群を含む);斉次,非斉次の線形群;相対論で用いるLorentz(ローレンツ)群, Poincare(ポアンカレ)群;などである.これらのどの群も,それぞれの空間で,不変量(保存量)の集合と結び付けられている.しかし,その変換群が成り立つ対称の性質がどのようなものであろうとも,また変換そのものがどのような性質であろうとも,すべての変換群には,抽象群の公理的定義を満たす共通の特性が存在する*.
--------------------------------------------------------------
*群論の基礎の平易な説明は,例えば,P.S.Aleksandrov(アレクサンドロフ)の本(1951)を見よ.
---------------------------------------------------------------
何らかの性質の元 $$g_{1},g_{2}, \ldots $$の集合が,群{$$g_{1},g_{2}, \ldots$$ }$$=G $$を作るとは,この集合で結合的な《積》という演算($$G$$中の任意の2元$$g_{i},g_{j} \in G$$の対に,元$$g_{k} \in G$$を対応させる:$$g_{i}g_{j}=g_{k}$$)が定義でき,次の2つの条件を満足することである: a)集合$$G$$には,任意の$$g_{i} \in G$$に対して$$g_{i}e=eg_{i}=g_{i}$$となる単位元$$e$$が存在する.b)任意の$$g_{i}$$に対して,$$g_{i}g_{i}^{-1}=g_{i}^{-1}g_{i}=e$$となる逆元$$g_{i}^{-1}$$が集合$$G$$に存在する.まとめると次の4条件になる.
Ⅰ. $$g_{i},g_{j} \in G$$ なら,$$g_{i}g_{j}=g_{k} \in G$$
Ⅱ. $$\left( g_{i}g_{j} \right) g_{k}=g_{i}\left( g_{j}g_{k} \right) $$
Ⅲ. $$g_{i}e=eg_{i}=g_{i}$$
Ⅳ. $$g_{i}g_{i}^{-1}=g_{i}^{-1}g_{i}=e$$
これらの関係は抽象群を定義する.Ⅰは$$G$$が演算に関して閉じていることを示し,Ⅱは結合法則,Ⅲは単位元の存在,Ⅳは逆元の存在を示す.積の演算を何にするかは,具体的な群に応じて定義する.
例:結晶群 $$2/m$$
群$$2/m$$に同型な置換群と直交行列群
有限図形の対称点群を定義している一様な直交変換の積は,これらの演算を引き続き行うことと理解する.この定義を用い,集合$$2/m$$では4つの群公理が満たされていることを確かめよう.
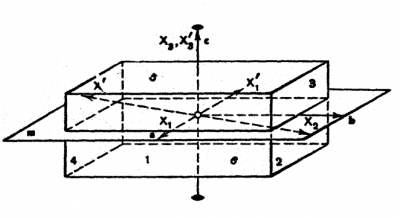
結晶点群$$2/m$$の対称を与えるのは,例えば,つぶれたマッチ箱の形(平行四辺形を底面とする直角プリズム)である.図203に示したごとく図形の面に番号をつける.図形の許される対称変換に対応する数字の置換を書くと:
$$1 \leftrightarrow \left( \begin{array}{@{\,} cccccc @{\, } }
1 & 2 & 3 & 4 & 5 & 6 \\[0mm]
1 & 2 & 3 & 4 & 5 & 6
\end{array} \right)$$ ,$$2 \leftrightarrow \left( \begin{array}{@{\,} cccccc @{\, } }
1 & 2 & 3 & 4 & 5 & 6 \\[0mm]
3 & 4 & 1 & 2 & 5 & 6
\end{array} \right) $$ ,$$\overline{1} \leftrightarrow \left( \begin{array}{@{\,} cccccc @{\, } }
1 & 2 & 3 & 4 & 5 & 6 \\[0mm]
3 & 4 & 1 & 2 & 6 & 5
\end{array} \right) $$ ,$$m \leftrightarrow \left( \begin{array}{@{\,} cccccc @{\, } }
1 & 2 & 3 & 4 & 5 & 6 \\[0mm]
1 & 2 & 3 & 4 & 6 & 5
\end{array} \right)$$
各置換の上の行には,自然の順序で数字が書かれている;下の行には,対称変換を行った後の順序が書かれている.例えば,軸2による180°の回転によって,面1は面3の位置に,面2は面4の位置に移ることなど明らかである.対称演算 $$1$$,$$2$$ ,$$\overline{1}$$ ,$$m$$ (対称要素と同じ記号で標す)と置換の間の対応は,1:1であり,それを両側向きの矢印で示した.得られた対応を使って,置換の積の演算を定義しよう.例として,右に書かれた演算を先に実行することにして,積 $$\overline{1}2$$ を求めてみよう:
$$\overline{1}2 \leftrightarrow \left( \begin{array}{@{\,} cccccc @{\, } }
1 & 2 & 3 & 4 & 5 & 6 \\[0mm]
3 & 4 & 1 & 2 & 6 & 5
\end{array} \right) \left( \begin{array}{@{\,} cccccc @{\, } }
1 & 2 & 3 & 4 & 5 & 6 \\[0mm]
3 & 4 & 1 & 2 & 5 & 6
\end{array} \right) =\left( \begin{array}{@{\,} cccccc @{\, } }
1 & 2 & 3 & 4 & 5 & 6 \\[0mm]
1 & 2 & 3 & 4 & 6 & 5
\end{array} \right) \leftrightarrow m$$
回転$$2$$ により面1は面3の位置に,反転$$\overline{1}$$ により面3は面1の位置に来る;従って,変換の積 $$\overline{1}2$$ は面1を面1に移す.同様にして,積 $$\overline{1}2$$ は面2,3,4を,それ自身に移すが,面5を面6に,面6を面5に移す.結局,変換の積 $$\overline{1}2$$ は,変換$$m$$ と同価である(等式の形で$$\overline{1}2=m$$と書く)という興味ある結果を得る.2つの演算の積$$g_{i}g_{j}$$ (右から左への順)を見つけていくと,結果を群$$2/m$$の乗積表の形にまとめることが出来る:
$$\begin{array}{c|cccc}
& 1 & 2 & \overline{1} & m \\[0mm]
\hline
1 & 1 & 2 & \overline{1} & m \\[0mm]
2 & 2 & 1 & m & \overline{1} \\[0mm]
\overline{1} & \overline{1} & m & 1 & 2 \\[0mm]
m & m & \overline{1} & 2 & 1
\end{array} $$ $$\begin{array}{c|ccc}
& \cdots & g_{j} & \cdots \\[0mm]
\hline
\vdots & & \vdots & \\[0mm]
g_{i} & \cdots & g_{i}g_{j} & \cdots \\[0mm]
\vdots & & \vdots &
\end{array}$$
この表を見れば,今問題にしている図形(図203)で許される対称変換の集合が閉性の公理「任意の2つの変換の積はやはりこの集合に属する」を満たしていることがわかる.結合則「3つの積$$g_{i}g_{j}g_{k}$$において,積は右から左に行うということを守りさえすれば,どのように括弧をつけてもかまわない」が満たされることを確かめることもさして困難ではない.群の単位元として働くのは恒等変換$$1$$ である.表から,$$2/m$$の各元に対して逆元が存在することもわかる(各元は自分自身が逆元になっている:$$g_{i}g_{i}=1$$).
表を用いれば,演算を繰り返し行った結果を知ることもできる.例えば,演算$$2$$ の3乗は演算$$2$$ に等しいことがわかる:
$$2^{3}=2 \cdot 2 \cdot 2=2^{2}2=2$$, ただし,$$2^{2}=2 \cdot 2=1$$ を用いる.
同一の結果になる演算の冪は同一と見なすから,群$$2/m$$は4つの異なった演算から成ることになり,位数は4となる.
$$2/m=\left\{ 1,2,\overline{1},m \right\} $$
群$$2/m$$の生成元として$$1$$ を含まない任意の元の対をとることができる.生成元 に対する定義関係 $$2^{2}=1$$,$$m^{2}=1$$,$$2m=m2$$ が与えられれば,元 $$m$$,$$2$$,$$2m=\overline{1}$$ をかけ合せることにより,群$$2/m$$の乗積表を完全に作ることが出来る.
上で調べた対称演算と6つの数字の置換の対応から,対称群$$2/m$$と4つの置換から成る群とが同型となる.一般に,群$$G=\left\{ g_{1},g_{2}, \ldots \right\} $$ と $$F=\left\{ f_{1},f_{2}, \ldots \right\} $$とは,元間に1:1対応があり乗積表が一致するとき同型であるという.すなわち
$$g_{i} \leftrightarrow f_{i}$$,$$g_{j} \leftrightarrow f_{j}$$ なら,$$g_{i}g_{j} \leftrightarrow f_{i}f_{j}$$
群が同型であることが判ると,積の法則とこれから導かれるような結論は,すべて1つの群について確認されたものなら,同型の群に移し変えることができる.これは研究の範囲が限定できるということである.Cayley(ケイリー)の定理「あらゆる有限群は適当な置換群と同型である」が成り立つため,有限群の研究は置換群の研究に帰着する.
置換群の集合は,直交結晶群の集合より大きい.例えば置換$$P=\left( \begin{array}{@{\,} cccccc @{\, } }
1 & 2 & 3 & 4 & 5 & 6 \\[0mm]
4 & 3 & 6 & 2 & 5 & 1
\end{array} \right) $$ の冪で作られる位数5の巡回群,すなわち群$$\left\{ P, P^{2}, P^{3}, P^{4}, P^{5} \right\} $$ ,
ただし$$P^{5}=\left( \begin{array}{@{\,} cccccc @{\, } }
1 & 2 & 3 & 4 & 5 & 6 \\[0mm]
1 & 2 & 3 & 4 & 5 & 6
\end{array} \right) =1$$,は結晶群のどれとも同型でない.
逆に,結晶群は置換群とのみ同型という訳ではない.結晶物理への応用で重要な,直交変換に同型な3次の直交行列群を考察しよう.我々の図形の結晶軸$$a, b, c$$と直交座標系$$X_{1}, X_{2}, X_{3}$$の関係は図203に示してある.図形のすべての対称変換それぞれに対応して座標系の変換がある.例えば,回転群$$2$$は軸$$X_{1}, X_{2}, X_{3}$$ を$$X_{1}^{ ' }, X_{2}^{ ' }, X_{3}^{ ' }$$ にもちきたす.行列要素を$$D_{ij}=cos\left( X_{i}^{ ' }, X_{j} \right) $$ で定義すれば,3次の行列
$$\left( \begin{array}{@{\,} ccc @{\, } }
D_{11} & D_{12} & D_{13} \\[0mm]
D_{21} & D_{22} & D_{23} \\[0mm]
D_{31} & D_{32} & D_{33}
\end{array} \right) $$ を得る.
回転2 を表すのは$$\left( \begin{array}{@{\,} ccc @{\, } }
-1 & 0 & 0 \\[0mm]
0 & -1 & 0 \\[0mm]
0 & 0 & 1
\end{array} \right) $$ となる.
同様にして,以下の行列と対称変換の対応が定まる:
$$1 \leftrightarrow \left( \begin{array}{@{\,} ccc @{\, } }
1 & 0 & 0 \\[0mm]
0 & 1 & 0 \\[0mm]
0 & 0 & 1
\end{array} \right) , \overline{1} \leftrightarrow \left( \begin{array}{@{\,} ccc @{\, } }
-1 & 0 & 0 \\[0mm]
0 & -1 & 0 \\[0mm]
0 & 0 & -1
\end{array} \right) , m \leftrightarrow \left( \begin{array}{@{\,} ccc @{\, } }
1 & 0 & 0 \\[0mm]
0 & 1 & 0 \\[0mm]
0 & 0 & -1
\end{array} \right) $$
良く知られた行列の積の定義(左の行列の行と右の行列の列を乗ずる:
$$D_{ij}=D_{i1}D_{1j}+D_{i2}D_{2j}+D_{i3}D_{3j}$$)を使い,演算の積に対応する行列の積を見つけよう:
$$\overline{1}2 \leftrightarrow \left( \begin{array}{@{\,} ccc @{\, } }
-1 & 0 & 0 \\[0mm]
0 & -1 & 0 \\[0mm]
0 & 0 & -1
\end{array} \right) \left( \begin{array}{@{\,} ccc @{\, } }
-1 & 0 & 0 \\[0mm]
0 & -1 & 0 \\[0mm]
0 & 0 & 1
\end{array} \right) =\left( \begin{array}{@{\,} ccc @{\, } }
1 & 0 & 0 \\[0mm]
0 & 1 & 0 \\[0mm]
0 & 0 & -1
\end{array} \right) \leftrightarrow m$$ , etc.
結局,対応する行列群と群$$2/m$$とは同型となる.
行列群を用いると,3次元空間における点あるいはその位置ベクトルの座標変換が記述できる.例えば,斉1次変換は,3つの等式の形にも,行列の形にも書くとことが出来る:
$$\begin{array}{@{\,} c @{\, } }
x_{1} ' =D_{11}x_{1}+D_{12}x_{2}+D_{13}x_{3} \\[0mm]
x_{2} ' =D_{21}x_{1}+D_{22}x_{2}+D_{23}x_{3} \\[0mm]
x_{3} ' =D_{31}x_{1}+D_{32}x_{2}+D_{33}x_{3}
\end{array}$$ または $$\left( \begin{array}{@{\,} c @{\, } }
x_{1} ' \\[0mm]
x_{2} ' \\[0mm]
x_{3} '
\end{array} \right) =\left( \begin{array}{@{\,} ccc @{\, } }
D_{11} & D_{12} & D_{13} \\[0mm]
D_{21} & D_{22} & D_{23} \\[0mm]
D_{31} & D_{32} & D_{33}
\end{array} \right) \left( \begin{array}{@{\,} c @{\, } }
x_{1} \\[0mm]
x_{2} \\[0mm]
x_{3}
\end{array} \right) $$
$$D$$で行列$$\left( D_{ij} \right) $$ を,$$r$$で$$x_{1}, x_{2}, x_{3}$$ のベクトルを標せば,この等式はもっと簡潔なテンソルあるいは演算子の形に書くことができる:
$$x_{i} ' =D_{ij}x_{j} , (i,j=1,2,3)$$ または,$$r '=Dr$$
(テンソル方程式で繰り返される添え字$$j$$は,1から3までの和を意味する:
$$x_{i} ' =D_{i1}x_{1}+D_{i2}x_{2}+D_{i3}x_{3}$$ ここで,$$i=1, 2, 3$$)
群のいくつかの性質
部分群.商群.群の準同型対応.
$$H=\left\{ h_{1},h_{2}, \ldots \right\} $$が,群$$G=\left\{ g_{1},g_{2}, \ldots \right\} $$ の部分群と呼ばれるのは, $$H$$が$$G$$の部分集合であり,かつ$$G$$の演算に関して群を作るときである.そのような性質は,例えば,結晶群$$2/m$$の部分群:$$ 1=\left\{ 1\right\}, 2=\left\{ 1, 2 \right\} , \overline{1}=\left\{ 1,\overline{1} \right\} , m=\left\{ 1,m \right\} $$で確かめることができる.有限群のすべての部分群は, Lagrange(ラグランジュ)の定理《有限群$$ G $$ の部分群$$H$$ の位数は,$$G$$の位数の約数である》によって,容易に見つけることが出来る.部分群$$H=\left\{ h_{1},h_{2}, \ldots \right\} $$の元は,同時に群$$G=\left\{ g_{1},g_{2}, \ldots \right\} $$の元でもある.このため,必然的に,群とその部分群は共通の単位元をもつ.これを,$$h_{1}=g_{1}=e$$ としよう.群$$G$$ の部分群$$H$$ を決めれば,我々は,左(右)剰余類を定義することができる. $$g_{i}H=\left\{ g_{i}h_{1},g_{i}h_{2}, \ldots \right\} $$または $$Hg_{i}=\left\{ h_{1}g_{i},h_{2}g_{i}, \ldots \right\} $$,ただし,$$h_{1}=e$$ ,元$$g_{i}$$ は部分群$$H$$ に属さない($$g_{i} \neq e$$,$$g_{i} \notin H$,$g_{i} \in G$$).1つの剰余類に属す元は全て異なり, $$g_{i} \neq g_{j}$$ならそれぞれの剰余類$$g_{i}H, g_{j}H$$の元もまたすべて異なることを示すことが出来る.これを用いれば,部分群に関して,群を展開し,すなわち,各剰余類に群の元を分類することができる.もし,群$$G$$ が有限(位数$$ n $$ )ならば,部分群$$H \subset G$$ は有限なる位数$$m<n$$ をもつ.従って,群$$G$$ の,例えば,左剰余類での展開は有限回で尽きる.
$$G=g_{1}H \cup g_{2}H \cup \ldots \cup g_{j}H=\left\{ h_{1},h_{2}, \ldots ,h_{m} \right\} \cup \left\{ g_{2}h_{1},g_{2}h_{2}, \ldots ,g_{2}h_{m} \right\} \cup \ldots $$
$$ \ldots \cup \left\{ g_{j}h_{1},g_{j}h_{2}, \ldots ,g_{j}h_{m} \right\} $$
群$$2/m$$の場合には,部分群$$2$$に関する展開は次のようになる.
$$2/m=1\left\{ 1,2 \right\} \cup \overline{1}\left\{ 1,2 \right\} =\left\{ 1,2 \right\} \cup \left\{ \overline{1},m \right\} $$
部分群に関する群の展開での剰余類の数$$j$$を部分群の指数という.あきらかに,群$$2/m$$の部分群$$2=\left\{ 1,2 \right\} $$の指数は2である.
部分群$$H \subset G$$は,もしこの部分群に関する右と左の剰余類が一致するなら,不変部分群または正規部分群と呼ばれる($$H \vartriangleleft G$$ と書く):$$Hg_{i}=g_{i}H $$ ($$g_{i} \in G$$,$$H \vartriangleleft G$$)
群$$2/m$$の部分群$$2$$は正規である.なぜなら,$$\overline{1}\left\{ 1,2 \right\} =\left\{ 1,2 \right\} \overline{1}$$ となるからである.可換性 の条件$$Hg_{i}=g_{i}H$$から,新たな群,商群が定義できる.これを$$G/H$$と標記する.商群の元となるのは,左(あるいは右)剰余類である:(左)剰余類の場合の積則を次のように定式化する: $$g_{i}H \cdot g_{j}H=g_{i}g_{j}H$$ ($$g_{i}g_{j}H=g_{k}H$$,ただし$$g_{i}g_{j}=g_{k}$$ )
可換性の条件は,$$g_{j}$$ を$$H$$ の右側から左側に移すときに使われた.$$g_{1}=e$$ とすると,有限指数$$j$$ の部分群に関する商群$$G/H$$ の乗積表は次のようになる:
$$\begin{array}{c|cccc}
& g_{1}H & g_{2}H & \ldots & g_{j}H \\[0mm]
\hline
g_{1}H & g_{1}H & g_{2}H & \ldots & g_{j}H \\[0mm]
g_{2}H & g_{2}H & g_{2}^{2}H & \ldots & g_{2}g_{j}H \\[0mm]
\ldots & \ldots & \ldots & \ldots & \ldots \\[0mm]
g_{j}H & g_{j}H & g_{j}g_{2}H & \ldots & g_{j}^{2}H
\end{array}$$
特に,商群$$(2/m)/2$$の乗積表は次のようである.
$$ \begin{array}{c|cc} & \left\{ 1,2 \right\} & \left\{ \overline{1},m \right\} \\[0mm] \hline \left\{ 1,2 \right\} & \left\{ 1,2 \right\} & \left\{ \overline{1},m \right\} \\[0mm] \left\{ \overline{1},m \right\} & \left\{ \overline{1},m \right\} & \left\{ 1,2 \right\} \end{array} $$
商群の概念は,群論において最も重要なものであり,無数の応用が存在する.群論におけるもう1つの重要な概念は,大きい群$$G=\left\{ g_{1},g_{2}, \ldots \right\} $$から小さい群$$F=\left\{ f_{1},f_{2}, \ldots \right\} $$ への準同型写像である.この写像は一方向で,次のように定義される:
$$g_{i} \to f_{i}, g_{j} \to f_{j}$$ なら $$g_{i}g_{j} \to f_{i}f_{j}$$
群が準同型なことは,記号$$G \to F$$ で標す.正規部分群$$H$$ に関する商群$$G/H$$は群$$G$$の準同型像であることを示すことができる:$$G \to G/H$$ これらの群の準同型は,群$$G$$の元$$g_{i}$$ を商群$$G/H$$ の元$$g_{i}H$$ に一方向に対応させることにより得られる:
$$g_{i} \to g_{i}H$$,$$g_{j} \to g_{j}H$$,$$g_{i}g_{j} \to g_{i}Hg_{j}H=g_{i}g_{j}H$$
このような対応の1方向性は,1つの剰余類が,$$G$$のいくつかの元と対応する.例えば,$$g_{1}^{*}=g_{i}h_{1}, g_{2}^{*}=g_{i}h_{2}, \ldots , g_{m}^{*}=g_{i}h_{m}$$ $$\left( h_{1}, h_{2}, \ldots , h_{m} \in H \vartriangleleft G, g_{i} \notin H, g_{i} \in G \right) $$が剰余類$$g_{j}H$$ に属することによる.
準同型対応があると,群$$G$$における積法則の研究を,小さい群$$G/H$$における積法則の研究に帰着させることが可能になる.
準同型写像は物理学で応用される群$$G$$の既約表現というものに関係がある.まずこれは演算子あるいは行列の群であつて,これらが準同型写像で表現している群$$G$$の積法則を保存しているような群である.