反対称の空間群(Shubnikov群)Ш
-古典空間群(Fodorov群)Фの拡大,あるいは並進群Tの拡大-
反対称空間群(Shubnikov群)の古典空間群(Fodorov群)に対する関係は,反対称結晶点群が結晶点群に対する関係と同様である.3次元のShubnikov群では,古典的な運動演算のすべて$$\phi _{i} \in \mit\Phi $$ に加えて,結合された演算$$ ш_{i }=\phi _{i}1'=1'\phi _{i} $$として定義される反対称演算$$ ш_{i } \in Ш $$とも出会う.これらのすべての演算をあらわな形にかくと:
運動演算 反対称運動演算
$$ \begin{array}{ccccc} 1 & 2 & 3 & 4 & 6 \\[0mm] \overline{1} & m & \overline{3} & \overline{4} & \overline{6} \\[0mm] \tau & 2_{1} & 3_{1} & 4_{1} & 6_{1} \\[0mm] & a & 3_{2} & 4_{2} & 6_{2} \\[0mm] & b & & 4_{3} & 6_{3} \\[0mm] & c & & & 6_{4} \\[0mm] & d & & & 6_{5} \\[0mm] & n & & & \end{array} \begin{array}{ccccc} 1' & 2' & 3' & 4 ' & 6 \\[0mm] \overline{1}' & m' & \overline{3}' & \overline{4}' & \overline{6}' \\[0mm] \tau ' & 2'_{1} & 3'_{1} & 4'_{1} & 6'_{1} \\[0mm] & a' & 3'_{2} & 4'_{2} & 6'_{2} \\[0mm] & b' & & 4'_{3} & 6'_{3} \\[0mm] & c' & & & 6'_{4} \\[0mm] & d' & & & 6'_{5} \\[0mm] & n' & & & \end{array} $$
この表で,$$ n_{j}$$の下添字はらせん軸のまわりのらせん回転を指定する.文字$$a,b,c,d,n$$ で,軸$$a,b,c$$ あるいは対角方向の映進面による映進を,文字$$\tau $$で並進部分群の任意のベクトル$$\tau \in T$$ を表す.また,$$3'=31'=1'3$$ などの記法も用いる.
空間群の演算リストを拡張した時に現れる反対称空間群は,Fodorov群を以下の演算の冪で生成される位数2の巡回群により拡大したものと見なせる:
$$ 1', \overline{1}', \tau '; 2', 2'_{1}, m', a', b', c', d', n'; 4', \overline{4}', 4'_{1}, 4'_{2}, 4'_{3} $$.*
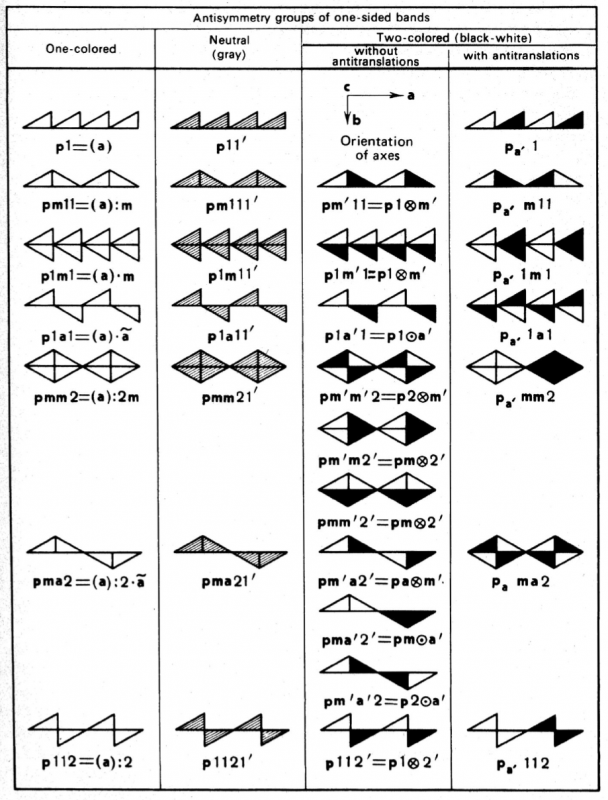
拡大の概念を知る手始めとして,1次元のShubnikov群(単面帯の反対称群)を例にとる.図208の第1列には単面帯の7つの古典空間群の国際記号を,並進軸$$a$$に沿って繰り返される単色図形(非対称三角形とそれらの組合せ)による幾何学模様と共に掲載した(図90,p160の表10参照).
---------------------------------------------------------------------------------------------------------------------------------------------------
*並進を含む演算は,2倍長さの並進を法とし群を生成する:
$$ \tau '\left( \textrm{mod}2\tau \right) =\left\{ 1,\tau ' \right\} ;2'_{1}\left( \textrm{mod}2\tau \right) =\left\{ 1,2'_{1} \right\} ; a',b',c',n'\left( \textrm{mod}\tau \right) =\left\{ 1,x \right\} ; d'\left( \textrm{mod}n \right) =\left\{ 1,d' \right\} ;$$
$$4'_{1}\left( \textrm{mod}2_{1} \right) =\left\{ 1,4'_{1} \right\} ; 4'_{2}(\textrm{mod}\left[ 2|\tau \right] =\left\{ 1,4'_{2} \right\} ; 4'_{3}\left( \textrm{mod}2_{1} \right) =\left\{ 1,4'_{3} \right\} $$, ここで,$$x=a', b', c', n'$$ $$ \tau \in T $$.
さらに,$$4'\left( \textrm{mod}2 \right) =\left\{ 1,4' \right\} ; \overline{4}'\left( \textrm{mod}2 \right) =\left\{ 1,\overline{4}' \right\} $$ が法により群になる.
---------------------------------------------------------------------------------------------------------------------------------------------------
2列目には,7つの中性群の具体化が,それらに応じた灰色図形を用い示されている.このタイプの群は,古典群と群$$1'=\left\{ 1,1' \right\} $$ の直積と考えることもできる. 3列目には,反恒等演算$$1'$$ と反並進演算$$\tau '$$ を含まない反対称群の象徴が示されている.このタイプの群は,古典群を群$$2',m',a'$$によって拡大したものと見なせ,黒白2色の図形で具体化することができる.(図208で,記号$$ \otimes $$と$$ \odot $$は,2つの点群の直積,および,点群と法による群 との条件直積を示している: 対応する空間群では半直積,条件半直積である.)
図208の最後の列には,反並進を含む単面帯の空間群の幾何学的具体化とその記号を示した.反並進$$\tau '$$で生成される群は,2倍の長さの$$(\tau '+\tau '=2\tau )$$単純並進を含むから,対応する並進と反並進の群を記号$$p_{\tau '}$$であらわす.記号 の下添字$$\tau ′$$は並進群 $$p$$の拡大を行なう反並進を示す.
読者は,次の文献に発表された群記号の表を調べながら,両面帯や柱の一次元Shubnikov群を,同様の方法で見つけるとよい(Shubnikov,1959,1962;Belov 他,1956,1962).この問題は,このくらいにして,我々は層の反対称Shubnikov群へと進もう.
そのような群は全部で528知られている(Neronova,Belov,1961).実例として,Weberの黒白図形(図184-187)に相当する80個の反対称群だけ調べてみよう.特にこれらの図形は,HeeschとShubnikovに反対称演算のような塗り変え演算の概念を思いつかせ,独立に,有限図形の反対称結晶点群を導出するに至らせた.
我々の考察の結果は,表16に示した.第1列には,表裏の面が同一色(黒または白)で塗られた1色層に対する17の古典空間群$$\mit\Phi$$の記号を載せた.第2列には,古典的1色群の生成元に,反恒等演算$$1'$$を結合して得た中性(灰色)群の記号を載せた;括弧内にはWeber図形(図184-187)に対応した番号が付けてある.全中性群$$Ш=\mit\Phi \otimes 1'$$は,古典群を群$$1'$$により拡大したものと見なせる.表の第3列には,2色Shubnikov群Шの記号を載せた.これは第1列目にあげたFodorov群$$\mit\Phi$$と同型である.これらの群Шは,反並進を含まず,指数2の古典部分群$$\mit\Phi ^{ \ast } \subset \mit\Phi $$ を反対称点群$$G'$$または法による反対称群$$G^{T'}$$により拡大したものと見なすことができる(直積 ,半直積,条件直積)*.
Ш$$=\mit\Phi ^{ \ast } \otimes G'$$,Ш$$=\mit\Phi ^{ \ast } \oslash G'$$,Ш$$=\mit\Phi ^{ \ast } \odot G^{T '} $$
しまいに,反並進$$\tau ′$$を含む2色Shubnikov群のカテゴリ-は,古典Fodorov群で,並進群 $$T \subset \mit\Phi $$の生成元に許される反並進の生成元$$\tau ′$$(並進群$$T$$の記号の下添字によって標示される)を結合することにより得られる.
従って,このタイプの群は,Ш$$=T_{\tau '}G$$ と標記されるが,古典群 $$\mit\Phi ^{ \ast }=TG$$を法による群$$\tau '(\textrm{mod}2\tau )=\left\{ 1,\tau ' \right\} $$で拡大したものと見なすことが出来る.
群Ш$$=T_{\tau '}G$$は,群Шと共通な並進群$$T$$を持ち,付加された並進ベクトル$$\tau $$が$$\tau ′$$と同じ長さ$$(\tau \leftrightarrow \tau ' )$$であるような古典群$$\mit\Phi =T_{\tau }G$$ と同型であることに注意しよう.群$$\mit\Phi ^{ \ast }=TG$$は,互いに同型なШ-群,Ф-群に共通な部分群(指数2)である.その上,群Ш$$=T_{\tau '}G$$は(生成元の違う選び方をすると)Ш$$=T_{\tau '}G'$$という表現も許される.この$$G' $$は反対称点群,あるいは,法による群(それぞれ,共型,あるいは,非共型Ш-群に対応);群$$G'$$は表の第1列に示した古典点群$$G$$または法による群$$G^{T}$$と同形である.この理由のために,Shubnikov群 Ш$$=T_{\tau '}G$$では,反並進なしのShubnikov部分群$$Ш^{*}=TG' \subset Ш =T_{\tau '}G $$を法による群で拡大したものとみなすことが出来る.
読者は,単面ネットワークパターン(図149)の対称群の投影と同様に,80のShubnikov層群に対し,対称と反対称の要素の投影図を作り,黒色と赤色で対称と反対称の要素を塗り分けてみるとよい.3次元Shubnikov群に対し同様な投影図を作れるだろう.
3次元Shubnikov群(Zamorzaev,1953,1957;Belov,他,1955)は,230のFodorov群$$ \mit\Phi $$を群$$1'$$で拡大し得られるタイプ $$\mit\Phi 1'=\mit\Phi \otimes 1'$$の230個の中性群:反並進$$\tau '$$や反恒等$$1'$$を含まない674個のタイプШ$$ =T \oslash G' $$ またはШ$$ =T \circ G^{T '} $$ の群:これらの群は並進部分群$$T$$の反対称点群$$G'$$あるいは同型な法による群$$G^{T '}$$での拡大とみなせる(それぞれ,共型,あるいは,非共型Shubnikov群に対応);Fodorov部分群$$\mit\Phi ^{*}=TG$$あるいは$$\mit\Phi ^{ \ast }=TG^{T}$$を反並進$$\tau '(mod2\tau )=\left\{ 1,\tau ' \right\} $$を法として拡大したタイプШ$$=T_{\tau '} \oslash G$$ あるいは$$T_{\tau '} \bigcirc G^{T }$$ の517の群;に区別される.230のFodorov群を形式的に含ませると,合計で230+230+674+517=1651のShubnikov群が得られる.図209(カラー挿入頁)には,反並進を含まない以下の3つの共型Shubnikov群の2色投影を例として掲載した.
$$ Ш_{10}^{44} : P2'/m=Pm \otimes \overline{1}' (P2/m/Pm)$$
$$ Ш_{10}^{45} : P2/m'=P2 \otimes \overline{1}' (P2/m/P2$$
$$ Ш_{10}^{46} : P2'/m=P\overline{1} \otimes m'=P\overline{1} \otimes 2' (P2/m/P\overline{1})$$
(記号$$Ш$$の添え字は、便覧《Shubnikov群》(koptsik,1966)の群の番号に対応させている.括弧中の記号は,いわゆる2項記号で,同型なFodorov群$$\mit\Phi$$(分子)と,同型なШ群とФ群に共有される指数2のFodorov部分群(分母)で定義される.
図210(カラー挿入)には,反並進を含む以下の3つのShubnikov群の2色投影図を示した.
$$ Ш_{10}^{47} : P_{a'}2/m=P2/m \circ a' (2P2/m/P2m)$$
$$ Ш_{10}^{48} : P_{c'}2/m=P2/m \circ c' (2P2/m/P2/m)$$
$$ Ш_{10}^{49} : P_{B'}2/m=P2/m \circ \displaystyle \frac{1}{2}\left( a+c \right) ' (B2/m/P2/m)$$
(記号$$a',c'$$は反並進ベクトルの方向を記述している.ベクトル$$\displaystyle \frac{1}{2}\left( a+c \right) ^{'}$$ は単位胞のB面心を記述しており,$$B'$$と標記される。$$ \circ $$は条件半直積;2項記号の前にある数字の意味は表17のノートに説明してある.)
Ш群の投影は次のようにして作れる.
直交変換による並進の積定理(あるいは,結晶学便覧)を利用して,
同型なFodorov群$$ \mit\Phi $$の対称要素の投影を鉛筆で描く;
この投影図で,古典部分群$$ \mit\Phi ^{*} $$の対称要素を黒い色で塗る;部分群$$ \mit\Phi ^{*} $$にない残りの対称要素(これは反対称の対称要素になる)は,赤色に塗る.対称と反対称の投影と並べて,別の図面でШ群単位胞における非対称図形(4面体)の配置を示そう.反並進を含むШ群を作ることは,原理的には,Bravais格子と類比した2色格子が前もって作れるなら,簡単に実行できる.図211には,このような格子の22の図と,与えられた格子と共存できる最も高い対称性を持つ共型Shubnikov群の記号を導いてある.表17に,これらの格子に対応している並進群$$T_{\tau '}$$の拡大されたベクトル基底$$ \left\{ a,b,c,\tau ' \right\} $$を導いた(非単純格子に対して,基底は中心化並進をつないでいるベクトルの過剰数を示している).同型な古典群への移行 $$T_{\tau }=\left\{ a,b,c,\tau \right\} \leftrightarrow \left\{ a,b,c,\tau ' \right\} =T_{\tau '}$$は,反並進ベクトル$$\tau '$$を普通のベクトル$$\tau $$に換えて行われる.表17には,古典部分群$$T^{ \ast }=\left\{ a,b,c \right\} $$(群$$T_{\tau '}$$と$$T_{\tau }$$とに共に同型)のベクトル基底と並進群の2項記号$$T_{\tau }/T^{ \ast }$$が示してある.これらの記号の基礎は,空間群$$ \mit\Phi/\mit\Phi^{ \ast } $$の完全な2項記号である.それに従って,517のShubnikov群全部を作ることができる.
Ш$$=T_{\tau '}G \leftrightarrow T_{\tau }G=\mit\Phi$$ ($$\mit\Phi^{ \ast }=TG$$),あるいは,Ш$$=T_{\tau '}G^{T} \leftrightarrow T_{\tau }G^{T}=\mit\Phi$$ ($$\mit\Phi^{ \ast }=TG^{T}$$)