イスラムデザインの美しい壁紙をご覧ください.
pinterestからお借りたこのデザインは,Aziza(カタールのドーハを拠点とするアーティスト)によるものです.彼女は神聖幾何学とイスラムのパターンを研究しています.https://artofislamicpattern.com/#/6
この模様はとても魅力的で,イスラム模様の特徴がよく出ています.
色のグラデーションがとても素敵なのですが,ここでは幾何学の話をするので,色の区別ができない眼鏡をかけたと思って色は無視します.
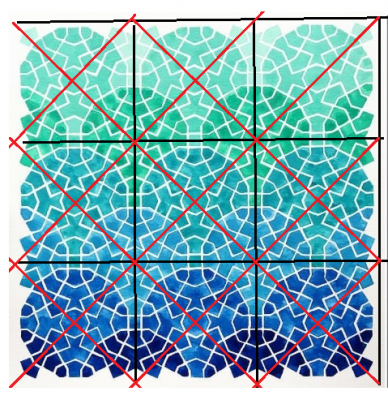
この壁紙の成り立ちを,表紙の図に示しました.この図の平面群(全部で17種類あります)は,$$p4mm$$と記号で書かれるものです.このような繰り返しパターンは,モチーフ(非対称要素)となる図形を,$$p4mm$$の対称操作で配置し構成されます.
壁紙模様で,まず目につくのは周期(格子)で,これを平面群の記述の先頭に書きます.この例では,記号で$$p$$と書きました.2次元のブラベ格子のタイプは$$p$$(plain=単純)と$$c$$(c-centred=c面心)の2つしかありません.そして,17種類の壁紙の対称性のうちの15種類が単純格子に分類されます.2次元の格子のタイプ分類(2次元のブラベ格子は5種類)は,前回の「ネットワーク・パターンの分類」で始めたところです(参照ください).
この壁紙模様の例では,すぐ,黒い正方格子が目につきます.しかも,正方形の中心にも格子点のある($$c$$面心格子)複合格子のように見えます.しかし,対角線の方向に目を配ると,一辺の長さが$$1/\sqrt{2}$$ になった,赤い正方格子($$p$$格子)が見えてきます.
始めに気づいたc面心格子(黒い格子)は「正方形」の対称性ですし,後で気づいた$$p$$格子(赤い格子)も「正方形」の対称性です.$$c$$面心格子を作れたように見えましたが,黒い格子を$$1/\sqrt{2}$$に縮小し45°回転すると赤い格子と同じものになります.正方格子のは$$p$$格子だけで,$$c$$面心格子は存在しないことがわかります.
この繰り返し模様のモチーフ(最小の非対称要素)は,赤い格子の1/8(黒い格子の1/16)の直角2等辺3角形です.このような3角形の模様付きタイルを作れば,そのタイル8つで赤い格子$$p$$格子の単位胞内を作ることができます.出来上がった単位胞を並べれば,無限に繰り返す壁紙模様が出来上がります.このモチーフは非対称要素と呼ばれるように対称性のない最小タイルです.
最後に,平面群の対称性の記法で,格子タイプ$$p$$に続く$$4mm$$は,格子点の対称性を記述する点群の記号です.
(注)平面群と点群の関係を正確に言うと:平面群は,格子を法とする準同型写像で点群に帰着します.