■企画講演(第4回)「虹の数学」を高校・大学で講義して,真島秀行(お茶の水女子大名誉教授)
講演者は,2002年から,高大連携プロジェクト,教養基礎の一環として,「虹の数学」を,附属高校1,2年生に開設しました.これは物理と数学の授業と連携して実施され,種々の現象の理解に数学が関わっていることを体験させることが狙いです.虹シート(ビーズ)などの教材があり虹の実験も行えるとのことです.
講演内容の詳細は,数学月間HPにリンクがありますので,youtube動画や資料pdfをご覧ください.ここに掲載する短い記事が,物理の視点から現象の理解を深め,数学へのガイドとなれば幸いです.
■幾何光学の視点
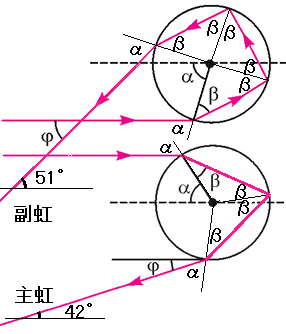
虹の現象は,幾何光学による理解と,波動光学による理解とがあります.まず,幾何光学による基礎的な知識から理解できることは,主虹の外側に副虹(主虹より遥かに暗い)が見えることの説明です.筆者が作成した模式図をご覧ください.これで,主虹と副虹が生じる原理がわかるでしょう.
太陽からの光は散乱角$$180°-φ$$の方向に散乱されて目に届きます($$φ$$ は散乱角の補角).
雨滴内部で1回反射して見える主虹の場合は,$$180°-φ=160°-6β+2α$$,2回反射して見える副虹の場合は,$$180°-φ=360°-6β+2α$$ で,屈折の法則,$$sinα/sinβ=n$$(水の屈折率は,可視光域で,$$n=4/3$$に近い)を用いて計算すると,主虹と副虹の場合,それぞれ,角度$$φ=42°,φ=51°$$ が得られます.しかし,目に届く光線はキッチリ角度$$φ$$ だけに来るわけではありません.太陽からは平行光線が雨滴に入射しますが,雨滴の球表面の曲率のため入射点で入射角 $$α$$は変化します.そのため光線の屈折経路は図示した1本ではなくそのまわりに拡がります.光線の集まる「焦点」は非点収差のために「火面」と呼ばれる拡張された概念になり,火面の形は光線束の包絡面になります.幾何光学での説明はここまでです.幾何光学だけでは,主虹と副虹で色の配列順番が逆転することは言えても,波長による屈折率の変化(光の分散)を語るには,波動論の概念が必要です.
■波動光学の視点
波長と分散,位相と干渉などの現象は,本来,光の波動論で導入できる概念です.可視光の波長は,雨滴直径の1/1000程度になります.
雨滴球内を進む波面の形状は,ホイヘンスの原理から説明でき,火面の各点を波源とし生ずる球面波を,位相のずれを考慮し重畳して得られる同位相の波面フロントです.この波面フロントを位相面内の変位 (光線方向に垂直)の3次関数で記述したのがエアリーの功績です.雨滴から観測者までの距離は非常に大きいため,雨滴の波面フロント各点を波源とする球面波は観測位置ではほとんど平面波の重畳となります.この電場を表す式が次に示すエアリー積分です:$$A(\theta )=\displaystyle \int_{0}^{ \infty }\textrm{cos}\displaystyle \frac{\pi }{2}\left( x^{3}-\theta x \right) dx$$
.ここで, $$θ$$は光線に沿った視角の外れ量に比例した変数です.エアリー積分$$A(θ)$$ は光線電場の振幅ですので,$$θ$$ 方向に観測される虹の強度は $$|A(θ)|^2$$になります.小さい雨滴サイズが均一で,空気が奇麗で空気による吸収や散乱がないと,主虹のすぐ内側にかすかに色づいた過剰虹が観察できることがあります.過剰虹は,このような光の干渉の効果で生じるものです.
エアリー積分の数値計算は,被積分関数を級数に展開したもので行なわれましたが,収束が悪いためになかなか困難でした.
後に,ストークスはエアリー積分が解となる微分方程式の解の漸近挙動を研究しました.この近似手法は,量子力学のWKB解でも用いられています.