
数学月間の会SGKのURLは,https://sgk2005.org/ になりました.


数学月間の会SGKのURLは,https://sgk2005.org/ になりました.
公的統計は合理的な意思決定を行うための基盤となる国民にとって重要な情報です.米国や英国でも統計が政策の客観的な基礎になるので,統計調査を政府の管理下に置き重視していますが,日本でも同様です.統計法という法律(2007年に大幅な改正)は,国勢調査などの基幹統計調査での報告義務,かたり調査の禁止,地方公共団体による事務の実施などが決められています.しかし,政府の統計を監督する統計委員会は、総務省に置かれているので,政府からの独立性が懸念されます.
麻生太郎副総理・財務相は2015年10月の経済財政諮問会議(議長・安倍首相)で,「毎月勤労統計については,企業サンプルの入れ替え時には変動があるということもよく指摘されている」と発言しました.これはもちろん誤りではないのですが,2018年のサンプル入れ替えのときに,偏ったサンプリングによる数値上昇への忖度につながった可能性はあります.
統計調査は全数調査ではなく,サンプリングした集団に対して実施されます.このサンプル集団が元の集団の性質を代表しているとみなせるのは,サンプリングが完全にランダムであることが前提です.しかし現実には完全にランダムは不可能です.調査される側の意識も,自分が正規分布の1点と思うと気が進まないし,個人情報を出すのを嫌うので,予定したサンプル数がなかなか集まらない.結局,何らかの偏りがあるサンプル集合に,適切な補正をし現実に近づけます.このように,サンプル集合の採り方により,得られる統計数値は色々に変わり得ますが,もし,意図的な偏りも加わると処置なしです.数値への信頼はほどほどにしましょう.しかし,数値化されると独り歩きし都合の良い数値が政策に採用される懸念があります.
こうして考えると,問題は統計学や数学以前の所にあり,もともと一つの数値で表すことのできない社会の複雑な状態を,おおざっぱでも正しく把握する常識感覚が必要になります.庶民の実感する豊かさと,統計数値に乖離があるとすれば,サンプル集団は,社会状態を正しく代表していないのです.
東京都における「500人以上規模の事業所」については,全数調査の1,464事業所(平成30年)でなければいけないのに,概ね3分の1の491事業所のサンプリングでした(2004年1月から東京都では約3分の1のサンプリングをしていました).
平成16年以降,厚生労働省から東京都に対し,厚生労働省が抽出した事業所名簿を送付し,当該名簿に基づき抽出調査を行うこととしていました.このサンプリングはランダムだったのでしょうか?
大企業と中小企業の比率などを考慮して,補正により現実に近づけようと試みたようですが,首尾一貫した定義のサンプル集団ではないので,アベノミクスの成果と言われる賃金伸び率の数値比較があてにならなくなりました.毎年の伸び率比較には,同一定義のドメインで統計をとらなければ意味がありません.
日刊ベリタに掲載
補足)サンプル集合の大きさ(抽出率)と誤差
母集団の全数検査すれば正確な数値が得られますが,現実には実施不可能なのでランダムサンプリングによりサンプル集合を作ります.しかし,サンプル集合の大きさが小さいほど,誤差はさらに大きくなりますので,ある程度のサンプル数は確保しなければなりません.サンプル数を1/2にして得られた数値を2倍にすれば精度は同じだと言う大臣がおりますが,とんでもないことを言うものだ.
菱形12面体の見える万華鏡の作り方の話をしたことがありました.
今回は,ケルビン立体の見える万華鏡を作ります.
菱形12面体とケルビン立体は,下図のような形です.
この2つの多面体は,正6面体や正8面体と同じ対称性で,重要な形です.
どちらの多面体も空間に隙間なく詰め込むことができ,空間に詰め込んだ時に,
菱形12面体は立方面心格子,ケルビン立体は立方体格子を作ります.
■さて今回は,ケルビン立体の見える万華鏡を作ります.
互いに直角に交わる3枚鏡が切り取る全空間の1/8が,
この万華鏡の非対称領域であることはすぐわかります.
しかしながら,ケルビン立体には,
直角に交わる3枚鏡の2等分面も鏡とする対称性があます.
1/8の空間領域の中に,
それらを鏡とする万華鏡を作ると,1/16,1/24,1/48などの空間を
非対称領域とする万華鏡が作れます.
ここでは,3回対称性が残るように尊重して,1/8,1/24.1/48の
3種類の万華鏡を作りましょう.
*注)非対称領域とは,万華鏡の内部の物体を置く領域のことです.
この物体を,万華鏡の鏡映で広げていき,どれもケルビン立体の映像が生じます.
写真A:
3種類の万華鏡を並べました

写真B:
非対称領域1/8の万華鏡

写真C:
非対称領域1/24の万華鏡
写真D:
非対称領域1/48の万華鏡
3種類の万華鏡像で,それぞれに8個ある正6角形面の中をよく見ると,
面の分割数の違いに気づくでしょう.写真Bでは分割なしですが,写真Cでは3分割,写真Dでは6分割になっています.
平面は2次元ですから独立な並進ベクトルは2つ a, bです.従って,
a, bを2辺とする平行4辺形が平面を充填する並進の単位(単位胞)となります.
3つの並進ベクトルがとれる凸平行6辺形もタイル張りが可能ですが,
a, b, cの間に, c=b-aの関係があり,このうちで独立な並進ベクトルは2つです.
.
平面をタイル張りできる凸6角形の形は,
ここに示した平行6辺形を含むタイプの他に,
さらに2タイプあることを,ラインハルトが学位論文で証明しました(1918)
凸6角形タイルで平面の充填ができるものは,
以下に図示する3つのタイプです.
タイプ1:2つのタイルが並進の単位を作る
(凸平行6辺形はこのタイプに含まれる)
タイプ2:4つのタイルが並進の単位を作る
タイプ3:3つのタイルが並進の単位を作る
5角形タイルで平面張り詰め(タイリング)ができるタイルの形は,以前掲載したタイプの5角形タイルだけではありません.全部で15タイプあります.単位胞がたくさんの5角形タイルで構成される15番目のものは,コンピュータを用いて見つかりました.
■米国サンディエゴの主婦マジョリー・ライスが,タイル張り(タイリング)の問題を初めて知ったのは,1975年のScientific American誌のマーチン・ガードナーのコラムでした.平面をタイル張りできる「タイル」の形,別の言い方をすれば,一つのタイルで平面を分割する(テッセレーション)問題です.
平面のタイル張りは,任意の3角形,任意の4角形タイルで可能,凸7角形以上のタイルでは不可能です.凸6角形の場合は,平行6辺形の他にもあり,全部で3タイプのタイル形が可能なことは,ラインハルトが学位論文で証明しました(1918).残されたのは凸5角形の場合で,1975年時点のガードナーのコラムには,ラインハルトの5タイプと1967年にカーシュナーが発見した3タイプが掲載されています.カーシュナーの論文には,タイリングできる凸5角形タイプが他にないことの証明は省略されており,そして,実際にまだ新しいタイプがあったのです.
■以下は,Natalie Wolchoverの記事(Quantamagazine,2017)から引用
https://www.quantamagazine.org/marjorie-rices-secret-pentagons-20170711/
フロリダ州に生まれたマージョリは,1クラスだけの田舎の学校で年長の子供たちと一緒に学びました.彼女は勉強好きでしたが,高等学校で数学を学んだのは1年だけです.貧困と文化的規範のため,大学に進学するなど思いもよらない時代でした.1945年,彼女は結婚しワシントンD.C.に移り,幼い息子と一緒に、その地で商業デザイナーとして働きました.後にサンディエゴに移住します.
数学が楽しみで,黄金比とピラミッドに魅了されていたといいます.ライスは,子どもたちが学校に通っている間に自分も読めるようにと,息子達にScientificAmericanの定期購読を許しました.
この問題では,5角形タイルのタイプ分けがとても難しい.連続変形によりどちらのタイプにも属するタイルがあるし,同じタイプでも出来上がったパターンが全く違うように見えたりもする.新しいタイプであるかどうかの判定は,ライスもずいぶん苦労したに違いありません.数学的な背景がないので,独自の記法システムを開発し,数ヶ月で新しいタイプを発見したといいます.彼女は発見に驚き喜んで,自分の仕事をガードナーに送りました.ガードナーはそれをペンシルバニア州のモラヴィアン・カレッジのタイリング問題の専門家であるドリス・シャトシュナイダーに送ってくれました.
シャトシュナイダーは,ライスの発見が正しいことを確認しました.ライスのアプローチは,後にマイケル・ラオが新しいコンピュータ支援の証明に取り入れた手法と同じでした.ライスは,4つの新しい凸五角形タイプと,それらによるほぼ60種類のテッセレーションを発見しました.シャトシュナイダーの招待で,ライス夫妻は大学の数学会に出席し,聴衆に紹介されました.ワシントンにある数学協会のロビーの床タイルに彼女の五角形テッセレーションの1つが使われ,彼女の発見したエッシャー風の絵が見られるといいます.
コンピュータ支援の新証明法で,フランスの数学者 マイケル・ラオが,ライスが発見した4つを含む15(残りは,ジェームスIII,シュタイン,マンがそれぞれ1つづつ発見)の凸五角形タイプがすべてであることを証明しました.ライスは,2017年7月2日94歳で亡くなりました.認知症のため,五角形タイリングの物語がついに完結したのを知ることはなかったが,ガードナーの提起から数十年が経過していました.
2018年もあと数日になりました.今年も,いろいろなことがありました.
おつき合いいただき有難うございました.
皆様にとって,2019年は良い年になりますように.
数学と社会の架け橋=数学月間の会からのお知らせです.この会を,
数学好きの同好会ではなく,分野横断的な市民活動にしたいと思っております.
社会でどのような数学が使われているのか?
上滑りでも言葉遊びでもなく,基礎を踏まえ本質をとらえた,見通しの良い説明で,そこにある数学に気づくことを目指します.
特定非営利活動法人「数学月間の会」が,来年早々スタートし,会員募集をする予定です.多くの皆様のご参加を呼びかけます.
■球に近い正20面体は,5つの正多面体(プラトン立体)のうちで,
最も対称性が高い(面の数が多い)もので,正3角形の面が20個でできています.
正多面体とは,正多角形(正p角形)の面でできていて,どの頂点の周りも同数の面(q個の面)が会している立体です.この立体を,シュレーフリの記号で{p,q}と記述します.
正多面体(プラトン立体)は,正4面体{3,3},正8面体{3,4},正6面体{4,3},正12面体{5,3},正12面体{3,5}の5つしかないことは証明できますから,
面数20より多い正多面体が存在するはずはありません.
しかし,例えばゴルフ球のディンプルはいくらでもたくさん作れるように思えなす.
正多面体の面を分割し続けると,いくらでも球に近い正多面体が作れるように思うかもしれません.しかし,そのようなことが可能なはずがありません.
ここで作るいくらでも球に近い多面体は,面が正多角形からわずかに歪むので,正多面体ではないのです.
正20面体の1つの正3角形の面を4つの三角形に細分化します.このとき,中心の三角形は正3角形ですが,その周りの3つの3角形は正3角形から歪むのを確認ください.
以下,細分化の操作を繰り返すたびに,面の数は4倍ずつ増加します.そして,細分化された面で正3角形のものは,初めの正20面体の面の中心にあるものだけです.
だから,正20面体を細分化して,球に近い多面体を作っても,その対称性は正20面体と同一(細分化しても対称性は上昇しません).素性は隠せないのです.細分化された多面体の面は正3角形ではないので,細分化でできる多面体は正多面体ではありません.
(この細分化で用いたjavaプログラムは郡山彬氏が作成しました)
私はいくつかのゴルフ球のディンプルを調べましたが,
正多面体{4,3}の細分化の系列と,{5,3}の系列のものがありました.
「美しい図形と奇妙な空間」
東京ジャーミイ(代々木上原,東京)にある装飾です.左写真は祭壇の横にあります.
イスラム特有の美しい複雑な図形です.右の写真はステンドグラスです.
これらの図形の美しさの原因の一つは,これらの図形が黄金比だらけだからでしょう.
もう一つの原因は,折りたたまれた空間のような不思議感じがあるからでしょう.
図の一番左は辺の長さが黄金比の2等辺三角形です.
つまり底辺を1とすると,等しい2辺は1.618...
真ん中の図は,正5角形の中にできる星形で,
星の頂角は黄金比の三角形にでてくる頂角36°と同じです.
一番右の図は,この星型とこの星型を180°回転したものを重ね合わせたものです.
東京ジャーミイの美しい図形は,星形を2つ重ね合わせたものになっているのに
お気づきでしょうか.
星形を2つ重ねた図形の対称性はどのように記述しましょうか.
まず,星形の対称性は.点群5mです(5は5回回転対称軸,mは鏡映面).
重ねた図形には,2回回転対称軸2があるので部分群として点群2を含みます.
結局,2つの点群の直積として2⊗5m=10mmの点群になります.
あるいは,星形5mを「法」にすると,10回回転操作(36°の回転)は
{1,10(mod5m)}のような,位数2の点群としても理解できます.
この考え方は,奇妙なもので,36°回転を2回続けると元の星形に重なるから
振り出しに戻ったと見なすわけで,我々の3次元ユークリッド空間では
360°回転しないと元に戻らないのですが,この奇妙な空間があるとすると
2x36°=72°回転すると元に戻ることになります.
菱形12面体が見える万華鏡を作りましょう.少し厚手(0.25mmとか0.31mm)のミラー紙(B5版)が手に入ると,簡単に作れます.
菱形12面体とは図1のような形で,空間を隙間なく埋め尽くすことのできる形でもあります.
菱形面ABA'B'を底面にして,立体の中心Oを結んだピラミッドADA'B-Oが,
中心のまわりに12個集まるとできる立体です.
① ピラミッドABA'B-Oの側面OAB,OBA',OA'B,OB'Aを鏡面にした万華鏡を作ります.非対称領域1/12
② ピラミッドABA'B-Oの半分のABB'-OやABA'-Oでも万華鏡が作れます.非対称領域1/24
③ さらにそれらの半分のABH-Oも万華鏡が作れます.非対称領域1/48
菱形12面体の内部には立方体が含まれますので,
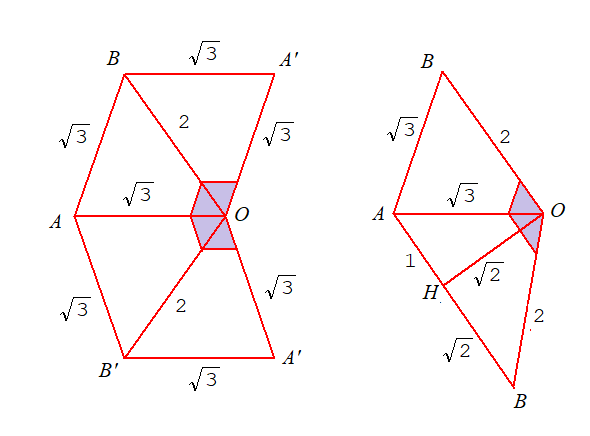
立方体の1辺を2とすると,菱形面ABA'B'の対角線の半分の長さは,
AH=1,BH=√2で,OH=√2,OA=√3,OB=2となります.
図 1 図2
底面(=菱形面ABA'B')と頂点(立体の中心O)を結びピラミッドABA'B'-Oを作ります.ピラミッドの内面を鏡面とし,外部(ピラミッドの底側)から頂点Oを覗く万華鏡です.
ピラミッドABA'B'-O,あるいは,底面が直角3角形ABHのピラミッドABH-Oの2種類の万華鏡ができます.ピラミッドの各所の寸法は図2に示します.この寸法を用いて,作った展開図を図3a,bに示します.どちらの展開図でも,Oの周りのグレーに塗った部分は切り取り,窓(=光の面)を開けます.それぞれの転開図で端辺どうし(左図ではOA',右図ではOB)を,それぞれ貼り合わせると完成(写真は図4a,b)です.
展開図のグレーに塗った部分は切り取りる.
図3a, 図3b
実際に作る寸法はこの4倍位にすると良い.
完成した万華鏡の外側.鏡面はピラミッドの内側.
図4a 図4b
(a)および(b)に対応する万華鏡像
■2つの万華鏡はどちらも菱形12面体像が見えます.図4aのピラミッドには図4bが4つ入ります(図4bの非対称領域は図aの1/4)ので,図4bの万華鏡の方が「菱形面に2mmの対称性があり」,図4aの万華鏡より対称性は高いのです.
■菱形12面体の見える他の万華鏡の例は,⇒ここに掲載します.
これらはすべて菱形12面体の見える万華鏡です.
非対称領域は,それぞれ,空間の1/8(写真1),空間の1/16(写真2,3),空間の1/32(写真4)です.1つの菱形面の中の分割数を観察すると,1(分割なし,写真1),2(写真2,3),4(写真4)であることからわかります.
写真1 写真2 写真3 写真4
トレチャコフ美術館展のポスターを飾る.19世紀末から20世紀初頭のロシア絵画の代表作,クラムスコイ作の「忘れえぬ女」は印象に残ります.表題のНеизвестнаяを直訳の「見知らぬ女」でなく「忘れえぬ女」とした翻訳は実に上手いですね.
この女性が誰だか謎です.すべてのものをありのままに見通すようなまなざしは,実に魅力的です.何も恐れず媚びず,勇敢にまっすぐにみる.あらゆる欺瞞を見抜いているようです.
トレチャコフ美術館展で気に入った絵画がありました.子供の世界のコーナーに展示されている「楽しいひととき」です.作者は,アントニーナ・レオナルドブナ・ルジェフスカヤ(女性).Антонина Леонардовна Ржевская
ルジェフスキー家のレオナルドの娘アントニーナというわけで,ロシアの標記では,父称からも姓からも女性ということがわかります.この絵画は,男名のА Л Ржевский と署名し1897年の展覧会に出品しました.
この絵画はパーベル・トレチャコフの目に留まり彼の所蔵となりました.
当時は絵画は男の仕事になっており偏見を心配したためです.
(注)父称や姓は,アントニーナ(女性名詞)を修飾する形容詞ですから女性の語尾変化をし,女性であることが明示されてしまいます.
彼女は没落した貧しい領主の家に生まれました.アレクサンドル2世による農奴解放令は1861年だが,農奴は土地を買わなければならなかったので不徹底改革でしたが,没落領主もあったでしょう.調べたら父は早く死に母と苦労したようです.
1880年にモスクワの絵画・彫刻・建築学校を卒業しました.
1899年に正式に移動派のメンバーになりました.
私立女子学校で教えたり,1920年には骨疾患の子供達のための教育芸術スタジオを組織しボランティア活動をしました.
「楽しいひととき」はこの絵です
忘れえぬ女
トレチャコフ美術館展のポスターを飾る.19世紀末から20世紀初頭のロシア絵画の代表作,クラムスコイ作の「忘れえぬ女」は印象に残ります.表題のНеизвестнаяを直訳の「見知らぬ女」でなく「忘れえぬ女」とした翻訳は実に上手いですね.
この女性が誰だか謎です.すべてのものをありのままに見通すようなまなざしは,実に魅力的です.何も恐れず媚びず,勇敢にまっすぐにみる.あらゆる欺瞞を見抜いているようです.
エントロピーといえばボルツマンを思い浮かべます.天才ボルツマン(オーストリアの物理学者)の墓碑には,S=klogWと刻まれているそうです.Sはエントロピー,Wはとり得る微視的な”状態数”,kはボルツマン定数です.
対数をとると,log(A・B)=logA+logBのように,積が和になりますので,加算量であるエントロピーと,微視的な”状態数”という積で増加する量とを結び付けるには,対数の登場となるわけです.
熱力学のエントロピーのクラウジウス(1865年)による定義は,系の温度をTとし,可逆過程で熱量δQが系に流入すると,dS=δQ/Tだけ系のエントロピーが増加するというものです.
系の内部エネルギーやエントロピーは状態量です.状態量ならば,系の2つの状態間で,変化経路にかかわりなく,状態量の差が一意に確定します.従って,系のある状態から出発し一回りして戻る経路積分をすると積分値はゼロです.状態量として系の内部エネルギーを例にとると,∲dE=0.このような性質のdEを全微分といいます.
熱や仕事の流入がないとき内部エネルギーは保存(熱力学の第一法則)されます.
閉じた系の内部で何か変化が起きても,その系のエントロピーは増大することはあっても減少することはなく,可逆変化の時のみエントロピーは不変(熱力学の第2法則)です.
系の微視的状態の数はW=N!/(n_1)!(n_2)!・・・(n_m)!通りで,ここで,P_iを状態n_iをとる確率(n_i=P_iN,Pi=1)とし,
スターリングの公式を用いlogWを近似すると logW=-(P_i)Nlog(P_i) が得られます.
情報エントロピーの定義もこれと同じ形になります.エントロピーを微視的な状態数の表現と解釈すれば,エントロピーが大きいと可能な状態数が多く,エントロピーが小さいとは予想がしやすいということです.