■第3日(8.7) 回折対称の上昇,松本崧生(金沢大学名誉教授)
結晶は原子で構成されており,原子を点と見做すと結晶は点の集合です.結晶の対称性(空間群で記述)は,点集合の対称性に他なりません.結晶で観測される現象の対称性には,その舞台となった結晶の対称性が反映されねばなりません(因果律).しかし,それを超える対称性を持つことを禁じているわけではありません.結晶によるX線回折という現象でも,結晶構造の点群を超えた回折対称(点群)が現れます.結晶からの散乱波は結晶構造のFourier変換であり,観測されるのは散乱振幅の絶対値の2乗(位相情報は失われる)であるので,回折強度像には必ず対称心が生じます(Friedel則).回折像の対称性にFriedel則を超えた対称の出現を回折対称の上昇と言います.観測される回折像の対称性が結晶構造の対称性と信じ込むと,誤った構造解析を進めることになります.
この問題は,結晶モデルとしての点集合の対称性と,点集合で定義されるベクトル集合(任意の2点を結び,そのすべての端点を原点に移動し重ねたもの)の対称性の関係と同値です.ただし,結晶は周期的構造なので点集合は有限集合を採用できますが,ベクトル集合では困難な問題が残されています.同一のベクトル集合を持つが,異なる点集合の構造となるものをホモメトリック構造と呼びます.
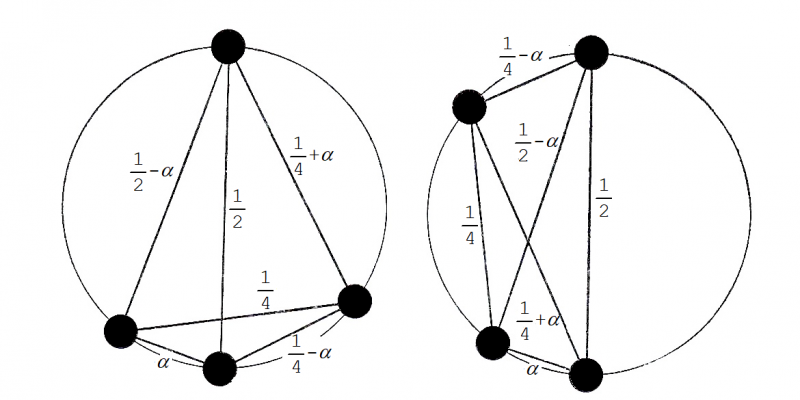
このような1次元構造を組み合わせて,2次元や3次元のホモメオリック構造を作れます.
1次元の8点系モデルで,ホモメトリック構造を系統的に導く講演者の研究が紹介されました.
回折対称の上昇は,空間群の対称要素を特殊点に作用させたときの同価点集合の対称性上昇と関係があります.空間群より高い対称を示す軌道をリストアップした講演者とWondratschekらの出版(1984,2015)「結晶空間群の非特性軌道」の紹介もなされました.


