11.一般化された対称群.反対称と色付き対称
古典結晶群を,群$$1′,2′,m′,\overline{1}′,4′(\textrm{mod}2), \overline{4}′(\textrm{mod}2)$$により拡大して作られる反対称結晶点群.
この章では,一般化された対称群の全タイプを,対応する古典群をある新しい群で拡大したものと見なすことにしよう.この新しい群には,冒頭に掲げた反対称群がある.ヘーシュ(Хееш; Heesch)(1929)とシュブニコフ(Шубников; Shubnikov)(1945)が独立に導びいた反対称の概念を,以下の例で紹介する.
一面が黒く,他面が白く染められた皮が与えられたとし,この黒-白の皮で折り返し付きの手袋を作ることにする.この問題は4つの解を持つことは明らかである(図205).即ち,次のものを作ることができる:1)右の白い手袋(黒い折り返し付き),2)左の白い手袋(黒い折り返し付き),3)右の黒い手袋(白い折り返し付き),4)左の黒い手袋(白い折り返し付き).右の手袋は,希望するなら,裏返しにして,左手にはめることができるし,左手の手袋も同様なことができるとする.従って,どの手袋でも,右にも,左にも,黒にも,白にもなれる.ここから,同一色の右と左の手袋だけを対称的に等しいと考えるのでなく,異なる色の手袋同志も等しい(反等価; антиравными; anti-equal )と考えるような概念の一般化が,全く自然に起こって来る.
図205.------------------------------
4つの反対称手袋:右白($$П^{+}$$),左白($$Л^{+}$$),右黒($$П^{-}$$),左黒($$Л^{-}$$).同じ色の手袋は対称演算で互いに変換し合い,異なる色の手袋は反対称演算で互いに変換し合う.
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
文字П,Лで右,左の手袋を,《+》,《-》で表面色の白,黒を標すことにし,手袋をある状態から他の状態へと変換する対称あるいは反対称の演算を見つけよう.一寸考えれば,次のことがわかる.$$Л^{+} \to П^{+} ,Л^{ - } \to П^{ - }$$の変換は,図205の手袋間に,垂直に$$m$$を想定し,これで反射させるか,任意の位置にある反転$$\overline{1}$$(ただし,手袋は図とは違った配置になる)によって実行される.変換$$Л^{+} \to Л^{ - } , П^{+} \to П^{ - }$$は,手袋の位置はそのままで,色を塗り変える演算で実行できる.この新しい演算を反恒等(антиотождествлением; anti-identification)と名づけ,1′と標記する.最後に,変換$$Л^{+} \to П^{ - } , Л^{ - } \to П^{+}$$は,垂直平面での反射と色の塗り変えを結合した(引続いて行なう)演算によるか,任意の位置にある反転と色の塗り変えを結合した演算によって実行できる.これらの新しい演算を,それぞれ反鏡映(антиотражением; anti-reflection),反反転(антиинверсией; anti-inversion)と名づけ,$$m'=m1'=1'm$$ ,および$$\overline{1}'=\overline{1}1'=1'\overline{1}$$と標記する.これらの演算に対応する対称要素を反対称面(плоскостью антисимметрии; anti-symmetry plane),反対称心(центром антисимметрии; center of anti-symmetry)と呼ぶことにし,記号$$m'$$と$$ \overline{1}′$$で標記する.
図206ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
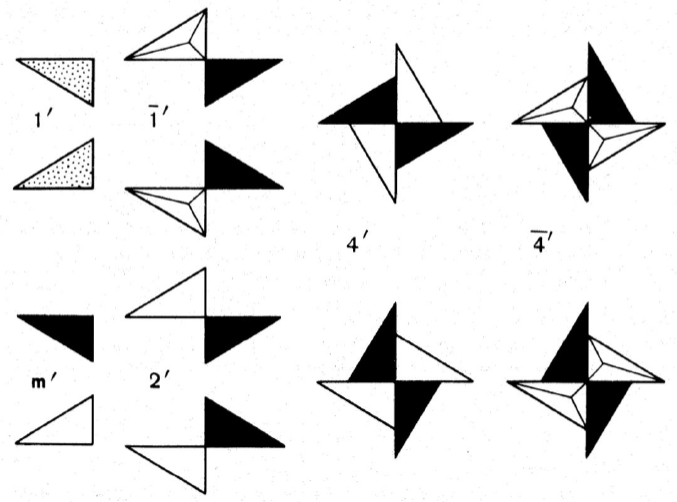
反対称群$$1′, m′, 2′, \overline{1}′,4′,\overline{4}′$$の(非対称4面体による)具体化図形.これらにより古典結晶群は拡大される.反恒等群$$1'$$では中性色(灰色)の4面体になるが,他の群では黒あるいは白の4面体で構成された図形になる.反対称演算は4面体の色の塗り変えを伴った幾何空間の変換である.4面体は観測者に頂点を向けているか底面を向けているかである.拡大を作るには,群$$4'$$や$$\overline{4}′$$の替わりに,モジュラス群$$4'(\textrm{mod}2)$$と$$ \overline{4}'(\textrm{mod}2)$$を用いれば十分である.
---------------------------------
図206には,観測者の方に頂点を向けたり,底面を向けたりしている非対称な4面体を集めて作った図形が示されている.もし,図形の白や黒の色を,正,負の電荷とか,何らかの物理量演算子(例えば,磁気モ-メントの演算子)の正,負の符号のような,図形に付加された超幾何学的特性と考えるなら,これら形而下の図形は,この節の冒頭にあげた反対称の巡回群(一つの演算の冪で生成される群)の表現図形《変換により不変な形而下の図形》となる.
位数2の群$$1'=\left\{ 1,1' \right\} $$は反恒等演算$$1'$$の冪で生成される.従って,群の定義関係は$$\left( 1' \right) ^{2}=1$$となる. 演算$$1'$$のあらゆる冪は,結果的には,中括弧内の元のどちらかに一致する.群が反恒等演算を含んでいるために,その表現図形は,同時に黒でもあり白でもある必要がある(物理的に中性).この理由で,群を具体化している右-,左-の4面体は中性色(灰色)に塗られている.
群$$m'=\left\{ 1,m' \right\} ,2'=\left\{ 1,2' \right\} ,\overline{1}'=\left\{ 1,\overline{1}' \right\} $$は,反対称平面での反射[$$\left( m' \right) ^{2}=1$$],反対称軸のまわりの180°回転[$$\left( 2' \right) ^{2}=1$$],反対称中心での反転 [$$(\overline{1}')^{2}=1$$]演算の冪でそれぞれ生成される.これらの群はすべて,抽象的には,群$$1'=\left\{ 1,1' \right\} $$に同型であるが,それらを具体化している図形は,物理的には,性質が異なっている.読者は,図206で,どこにそれぞれの反対称要素があるかを確かめよ.
群$$4'(\textrm{mod}2)=\left\{ 1,4' \right\} $$と$$ \overline{4}'(\textrm{mod}2)=\left\{ 1,\overline{4}' \right\} $$は,90°の反対称単純回転,あるいは反対称回映(回反)演算の冪で生成される.これらの群は,元の対応$$4' \leftrightarrow 4,\overline{4}' \leftrightarrow \overline{4}$$ (p.212)により,群$$ 4(\textrm{mod}2)=\left\{1, 4\right\} $$あるいは$$ \overline{4}(\textrm{mod}2)=\left\{1, \overline{4} \right\} $$と同型である.
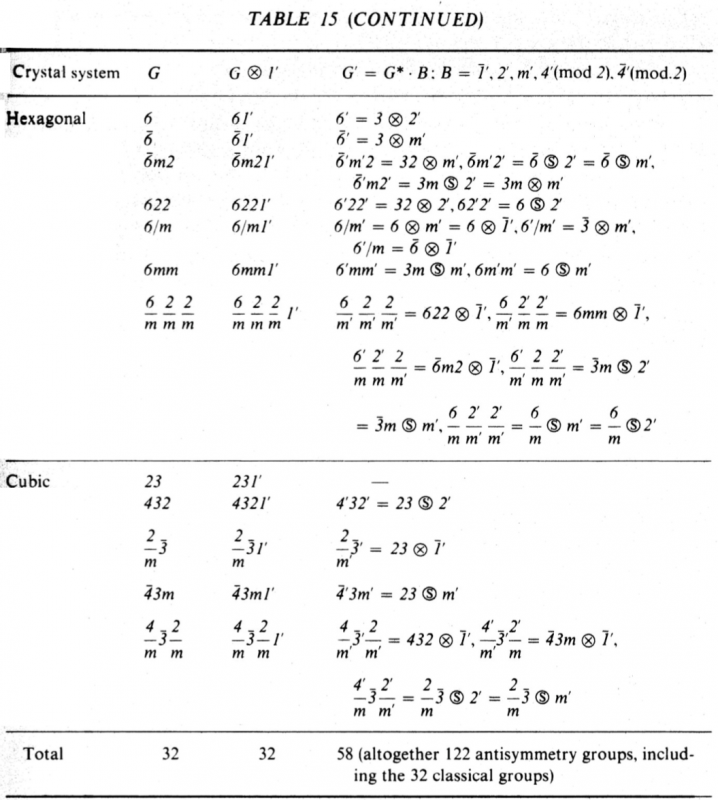
他の反対称結晶群は,すべて,上記の群による古典結晶群の拡大として作られる(表15).
32の中性群$$G1'$$は,結晶群の生成元に,反恒等演算を結合して,あるいは同じことであるが,群$$G={g_{1},g_{2}, \ldots ,g_{n}}$$を群$$1'=\{1,1'\}$$に《乗じて》 得られる.演算$$1$$との積では,どの演算$$g_{i}$$も変わらない.演算$$1'$$との積は結合された演算$$g_{i}'=g_{i}1'=1'g_{i}$$を作る(これを反対称演算と名づける).このように ,拡大群$$G1'$$の位数は,直積$$G1'=G \otimes 1'$$中の因子である始めの結晶群$$G$$の位数の2倍となる.
$$G1'=\left\{ g_{1},g_{2}, \ldots ,g_{n},g_{1}',g_{2}', \ldots g_{n}' \right\} =\left\{ g_{1},g_{2}, \ldots ,g_{n} \right\} \otimes \left\{ 1,1' \right\} $$,
ただし,$$g_{1}=1,g_{1}'=1'$$.
反恒等演算1′を含まない58の2色(黒-白)群 $$G'$$は,指数2の結晶部分群$$G^{*}\subset G$$を生成元にして,演算 $$\overline{1}′,2′,m′,4′,\overline{4}′$$を結合するか,同じことだが,群$$G^{*}$$の各演算を反対称群$$\overline{1} ′,2′,m′,4′(\textrm{mod}2), \overline{4}′(\textrm{mod}2)$$の演算に乗じて得られる.2倍の位数をもつこれらの群は,対称演算と反対称演算を同数づつ含むから,反対称の一般化された群G′では,直積(прямом; direct),半直積(полупрямом; semi-direct),条件積(условном произведении; quasi-direct)の因子である指数2の結晶部分群$$G^{*}=\left\{ g_{1},g_{2}, \ldots ,g_{n} \right\} $$は保存されている:
$$G'=\left\{ g_{1}, g_{2}, \ldots , g_{n}, g_{1}g', g_{2}g', \ldots , g_{n}g' \right\} =\left\{ g_{1}, g_{2}, \ldots , g_{n} \right\} \otimes \left\{ 1, g' \right\} $$,
ただし,$$g_{1}=1,g'$$は拡大を作る演算.
黒-白群$$G'$$が,同じ位数をもつ結晶群に同型となるのはすぐわかる.それぞれの群$$G'$$に対して,同型な結晶群$$G$$と指数2の古典部分群$$G^{ \ast }$$を指定すれば,反対称群$$G'$$の2項記号といわれるもの$$G/G^{ \ast }$$が得られる.この記号は,$$G'$$に関するあらゆる必要な情報を含んでいて,その群の分解を可能にする.
$$G'=G^{ \ast } \cup G^{ \ast }g'$$ $$(g' \neq 1')$$
つまり,対称演算と反対称演算の剰余類を類別して,反対称群の2色ステレオ投影が作れる.
表15には,58の群G′が直積$$( \otimes )$$,半直積$$( \oslash )$$,条件直積[準積]$$( \odot )$$の型で表現されている:$$G'=G^{ \ast } \cdot B$$,ここで$$B$$は群 $$\overline{1} ′,2′,m′,4′(\textrm{mod}2), \overline{4} ′(\textrm{mod}2)$$.直積のときには,各因子$$G^{ \ast }$$,$$B$$はどちらも他方の自己同型群になっている.いいかえれば,群$$G^{ \ast }$$の対称要素は群$$B$$の対称要素を$$B$$の中へ変換し,群$$B$$の対称要素についても同様である.しかし,半直積のときには,そのような働きは$$B$$だけにある.群$$G'$$に同型な群$$G$$の国際記号は,$$G'$$からダッシュを消せば得られる.図207に,例として,次の群に対する対称要素と非対称図形の同価系の2色ステレオ投影を与える:$$4'mm'-4mm/2m1$$,$$\overline{4}2'm'-\overline{4}2m/\overline{4}11$$,$$\overline{4}'2m-\overline{4}2m/221$$,$$\overline{4}m2'-\overline{4}m2/2m1$$.どの場合でも,2項記号中の群$$G^{ \ast }$$は,群$$G$$の方位をもっている.すなわち,群$$G'$$で対応する方位に,反対称軸や反対称平面の法線がある場合は,記号$$G^{ \ast }$$のその場所には1と書く.群の投影では,古典対称要素を黒で,反対称要素を赤で標示する.ここでは,反対称の演算は,図形の幾何学的変換と4面体の黒から赤(あるいはその逆)への塗り変えになる.
この例に倣い,古典群のステレオ投影(図69)を利用して,古典部分群$$G^{\ast}$$の 対称記号を黒く,残りの要素を赤く塗り分けることにより,反対称群の2色投影を作ることは,読者にとって良い練習となる.反対称群すべての2色投影と2項記号は,モノグラフ《Shubnikov群》(Koptsik,1966)に導かれている.このモノグラフは,これらの群の物理的応用に関連した群論的記述も含んでいる.
この節で作られた反対称群は,形而下の2色図形(またはこれらを取り囲んでいる3次元2色空間)の対称特性を記述する.この空間の点に記入されている超幾何学的な特性は,2つの値だけ取る色や任意の関数などで抽象的に表現される.一般点にあれば,その点は1つの色が確定するが,特殊点にあれば,その点の対称に従い2つの色が与えられる.もう一つの解釈(p197)は,これらの群を,超幾何学的座標(記号の上添え字)が,ただ2つの固定値$$ \pm x_{4}$$をとる非一様な4次元空間の対称群 $$G_{3,0}^{1}$$と考えることである.一様な4次元空間では,対称点群の数は58( $$G_{3,0}^{1}$$)でなくて227($$G_{4,0}$$ )となる(章末の文献を見よ).