第1章 群の概念
[定義]群
$$G=\left\{ a, b, c, \cdots \right\} $$ 集合$$G$$が群groupと呼ばれるのは,次の公理を満たす場合である:
0) $$a, b \in G$$, $$a \circ b \in G$$ 2項演算が定義される
1) $$\left( a \circ b \right) \circ c=a \circ \left( b \circ c \right) $$ 結合律
2) $$(a \circ e=)e \circ a=a$$ $$e$$:単位元,左単位元
ある元$$e$$(ただ一つ)が存在し,すべての$$ \forall a \in G$$に対して$$e \circ a=a$$が成り立つ.
3) $$ \forall a \in G$$に対して, $$(a \circ x=)x \circ a=e$$となる$$x$$が(ただ一つ)存在する.
$$x$$:$$a$$の逆元,左逆元
1)~3)を群の公理という.
[演習]群の公理の中で,”ただ一つ”というのは公理に含めなくてもよい(導くことができる).
■単位元が2つあったとし,それらを$$e, f \in G$$とする.
$$ \forall a \in G$$, $$a \circ f=f \circ a=a$$ ①
$$a \circ e=e \circ a=a$$ ②
$$e=f \circ e=e \circ f=f$$
① ②
■$$a$$の逆元が2つあったとし,それらを$$x, y \in G$$とする.
$$y \circ a=a \circ y=e$$, $$x \circ a=a \circ x=e$$
$$\left( y \circ a \right) \circ x=e \circ x=x$$
$$y \circ \left( a \circ x \right) =y \circ e=y$$
(注)これらの証明で,左単位元と右単位元(左逆元と右逆元)は同一ということが使われている.
[演習]
■ $$(a^{-1})^{-1}=a$$
(証明) $$a \circ a^{-1}=a^{-1} \circ a=e$$
$$(a^{-1}) \circ (a^{-1})^{-1}=(a^{-1})^{-1} \circ (a^{-1})=e$$
$$(a^{-1})$$の逆元は一意であるから,$$(a^{-1})^{-1}=a$$
■ $$\left( a \circ b \right) ^{-1}=b^{-1} \circ a^{-1}$$
(証明) $$(a \circ b)^{-1} \circ (a \circ b)=e$$
$$(b^{-1} \circ a^{-1}) \circ (a \circ b)=e$$
[定義]
$$G$$が可換群(Abel群) $$ \forall a, \forall b \in G$$, $$a \circ b=b \circ a$$
このときの演算$$ \circ $$は,乗法と呼ばずに加法$$+$$と呼ぶ.加法の単位元は”$$0$$”と呼ぶ.
無限群と有限群: 群$$G$$の元の数[群の位数]が無限か有限かによる.
[演習]
群の左単位元はまた右単位元でもある. $$^{ \exists }e, ^{ \forall }a$$: $$e \cdot a=a$$ → $$a \cdot e=a$$
元$$a$$の左逆元はまた右逆元でもある. $$^{ \exists }x, ^{ \forall }a$$: $$x \cdot a=e$$ → $$a \cdot x=e$$
(証明)
$$e \cdot e=e$$ → $$e$$は$$e$$の左逆元であり,かつ,右逆元であることを意味する.
$$a \cdot e=a \cdot (e \cdot a) \cdot a^{-1}=a \cdot a \cdot a^{-1}=a$$
★群の例
1. 整数$$Z=\left\{ 0, \pm 1, \pm 2, \cdots \right\} $$: 加法群をなす.
2. 実数$$R$$: 加法で群
3. $$R-{0}$$: 乗法で群
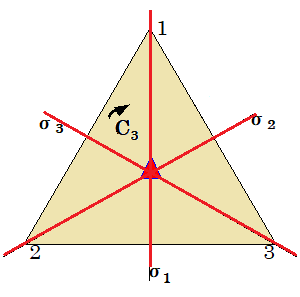
4. 正3角形の3次の対称群(置換群)
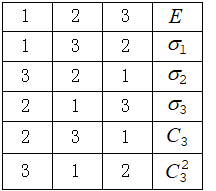
対称操作の表
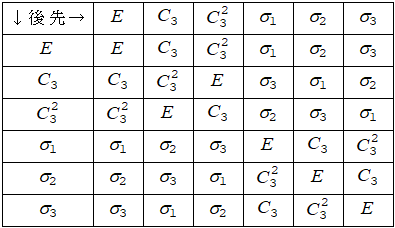
■乗積表
鏡映面$$\sigma _{1}, \sigma _{2}, \sigma _{3}$$は,図形のそれぞれの頂点に固定されて変換されるとして,群の乗積表を作りなさい.
乗積表
乗積表からわかること:
・群を作る$$ \longrightarrow $$ 3次の対称群(有限群,位数は6)
・可換群(Abel群)ではない.
5.$$n$$次正則行列の集合
6. $$n$$次直交行列 $$O(n)$$
$$A \in O(n)$$のとき,$$\left| \begin{array}{@{\,} c @{\, } }
A
\end{array} \right| $$を求めよ.$$\left| \begin{array}{@{\,} c @{\, } }
A
\end{array} \right| =\textrm{det}A$$は行列式の記号
$$\left| \begin{array}{@{\,} c @{\, } }
^{t}AA
\end{array} \right| =\left| \begin{array}{@{\,} c @{\, } }
E
\end{array} \right| $$ $$\Longrightarrow$$ $$\left| \begin{array}{@{\,} c @{\, } }
A
\end{array} \right| ^{2}=1$$ $$\Longrightarrow$$ $$A= \pm 1$$
これを回転群と呼ぶ.
■$$A \in SO(2)$$のとき,適当に$$\theta $$をとって,
$$A=\left( \begin{array}{@{\,} cc @{\, } }
\textrm{cos}\theta & -\textrm{sin}\theta \\[0mm]
\textrm{sin}\theta & \textrm{cos}\theta
\end{array} \right) $$ と書くことができる.
[定義] 元の位数$$r$$
元$$a$$の位数$$r$$とは,$$a^{r}=e$$となる最小の自然数である.
このような$$r$$がないときは,元$$a$$は自由元である.
-----------------------------
集合の2元間に或る2項演算$$ \circ $$が定義され,その演算$$ \circ $$に関して,或る「構造」を持つ集合を代数系といいます.
演算$$ \circ $$は結合法則 $$\left( x \circ y \right) \circ z=x \circ \left( y \circ z \right) $$が成立つ.
演算$$ \circ $$について,結合法則だけが存在する代数系を「半群」という.
-----------------------ーーーーーー
[定義]群の軌道
群$$\mit\Gamma $$を,集合$$X$$上に作用する「変換群」とします.
群$$\mit\Gamma $$による$$a \in X$$の軌道とは,$$\mit\Gamma (a)=\left\{ \sigma (a)|\sigma \in \mit\Gamma \right\} $$.
$$X \ni a, b$$に対して,$$b$$が$$a$$の軌道に含まれるという関係は,$$X$$における同値関係になる.
軌道は同値類である.集合$$X$$を軌道で類別できる.
$$X$$の中に軌道がただ一つしかない場合:
つまり,$$^{ \forall }x, ^{ \forall }y \in X$$に対して,$$^{ \exists }\sigma \in \mit\Gamma $$があり,$$\sigma (x)=y$$のとき,$$\mit\Gamma $$は推移的という.
[演習]軌道に属するという関係は,同値関係であることを確認せよ.
$$a$$に軌道に$$b$$が含まれるとせよ:$$b \in \left\{ \sigma (a)|\sigma \in \mit\Gamma \right\} $$であるから,$$b=\sigma _{i}(a)$$となる$$^{ \exists }\sigma _{i} \in \mit\Gamma $$がある.$$\mit\Gamma $$は群であるから,$$\sigma _{i}^{-1} \in \mit\Gamma $$があり,$$\sigma _{i}^{-1}(b)=a$$となり,$$b$$の軌道に$$a$$が含まれる.
ゆえに,$$\mit\Gamma (a)=\mit\Gamma (b)$$.これは,対称律を保証する.反射律,推移率も同様に成立する.