直積,半直積,条件積による群の拡大.
回転群の拡大としての結晶群.
与えられた部分群$$H$$を含む任意の群$$G$$を,$$H$$の拡大と呼ぶ.部分群(右剰余類)による展開を;
$$G=Hg_{1} \cup Hg_{2} \cup \ldots \cup Hg_{s}=\left\{ h_{1},h_{2}, \ldots ,h_{m} \right\} g_{1} \cup \left\{ h_{1},h_{2}, \ldots ,h_{m} \right\} g_{2} \cup \ldots $$
$$ \ldots \cup \left\{ h_{1},h_{2}, \ldots ,h_{m} \right\} g_{s}$$ (1)
とすると,展開から次のことがわかる.元 $$\left\{ g_{1},g_{2}, \ldots ,g_{s} \right\} $$が剰余類の代表系を作っているときは,群$$H$$の拡大$$G$$が存在する.これは次のことを意味する:
1°元$$h_{1}=g_{1}=e$$ は,$$G$$ にも$$H$$ にも共通な単位元である.従って,系$$\left\{ g_{1},g_{2}, \ldots ,g_{s} \right\} $$ の単位元でもある.
2°系$$\left\{ g_{1},g_{2}, \ldots ,g_{s} \right\} $$の元は,$$g_{j} \neq g_{l}$$ なら,剰余類$$Hg_{j} \neq Hg_{l}$$ すなわち任意の$$h_{i},h_{k} \in H$$ に対して,$$h_{i}g_{j} \neq h_{k}g_{l}$$ であるから,すべて異なる.
3°元$$h_{i}g_{j} \in Hg_{j}$$と$$h_{k}g_{l} \in Hg_{l}$$の積は,群$$G$$ の展開(1)に現れる或る1つの剰余類$$Hg_{q}$$ に含まれる.
条件1°,2°,3°は各剰余類から1つ1つ選んだ代表元の種々な組にも成り立つ.群$$H$$の同一の拡大$$G$$を導くこのようなすべての組を,我々は同値とみなす.群拡大定理*では,非同値な拡大$$G$$を作る非同値な代表系$$\left\{ g_{1},g_{2}, \ldots ,g_{s} \right\} $$ を見出す特別な方法が複数研究されているが,ここではその一部の紹介にとどめる.
------------------------------------------------------------------
*この説明は,A.G.Kurosh(クローシュ)(1970)やM.Hall(ホール)(1959)の一般群論の教科書に見られる.結晶群の拡大に関するZassenhaus(ツァセンハウス)(1948)やAscher(アッシャー)およびJanner(ヤンネル)(1965-1969)の研究にも見られる.非正規の拡大はB.L.Van der Waerden(バンデルワルデン)とJ.J.Burckhardt (ブルックハルト)(1961),A.M.Zamorzaeb(ザモルザエフ)(1967), V.M.Busarkin(ブサルキン)とYu.M.Gorchakov(ゴルチャコフ)(1968),V.A.Koptsik(コプツィク)(1967)の研究に見られる; V.A.Koptsik, G.N.Kotzev, Zh.N.M.Kuzhukeev(1973)が英語版では追加された.
------------------------------------------------------------------
最初に,もし展開(1)中の剰余類 を,積(2)が定義されている群の元$$\left\{ Hg_{1},Hg_{2}, \ldots ,Hg_{s} \right\} $$ とみなせるなら,条件1°,2°,3°は満たされていることに注意しよう.
$$Hg_{j} \cdot Hg_{l}=Hg_{q}$$ ($$Hg_{q} \neq Hg_{j} , Hg_{l}$$ ただし,$$g_{j}, g_{l} \neq g_{1}=e$$) (2)
非正規な拡大( $$H$$が群$$G$$の正規部分群でないとき)の一般の場合,これは剰余類の置換群となる.正規な拡大のときは,剰余類の代表元は条件1°,2°,3°の他に次の可換条件を満足しなければならない:
4° $$g_{j}H=Hg_{j}$$ または $$g_{j}Hg_{j}^{-1}=H$$
つまり,任意の$$h_{k} \in H$$ ,$$g_{j} \in G$$ に対して $$g_{j}h_{k}g_{j}^{-1} \in H$$
この場合,部分群$$H$$は$$G$$において不変あるいは正規となり,系$$\left\{ Hg_{1},Hg_{2}, \ldots ,Hg_{s} \right\} $$ は,商群$$G/H$$を作る.積則(2)は次のようになる.
$$Hg_{j} \cdot Hg_{l}=Hg_{j}g_{l}$$ (3)
剰余類の組が,積(2)あるいは(3)で群を作ると仮定すれば,条件3°は強められて,
$$h_{i}g_{j} \cdot h_{k}g_{l}=h_{p}g_{q} \in Hg_{q}$$ または $$ \in Hg_{j}g_{l}$$,ただし,$$h_{i}g_{j} \in Hg_{j}$$,$$h_{k}g_{l} \in Hg_{l}$$となる.
正規拡大の場合には,さらに進んだ結果が導かれる.元$$g_{j}$$を剰余類$$Hg_{j}$$に比較考察すると,各剰余類から1つづつ取った代表元の任意の組において,系$$\left\{ g_{1},g_{2}, \ldots ,g_{s} \right\} $$ は商群$$G/H$$と同型な群を作ることがわかる:
$$Hg_{j} \leftrightarrow g_{j} , Hg_{l} \leftrightarrow g_{l} , Hg_{j}g_{l} \leftrightarrow g_{j}g_{l}$$
同型の条件は,群\$$G$$の積則に現れる元の積$$g_{j}g_{l}=g_{n}$$ が,剰余類$$Hg_{n}$$ に属することを要請する.
$$g_{j}g_{l}=h_{jl,n}g_{n} \in Hg_{n}$$, $$h_{jl,n}=h_{1},h_{2}, \ldots ,h_{m} \in H$$, $$g_{n} \in \left\{ g_{1},g_{2}, \ldots ,g_{s} \right\} $$
一般に,$$h_{jl,n} \neq h_{1}$$のとき,元$$h_{jl,n}g_{n} \notin \left\{ g_{1},g_{2}, \ldots ,g_{s} \right\} $$である.還元積の法則
$$g_{j}g_{l}=h_{jl,n}g_{n} \equiv g_{n}\left( \textrm{mod}h_{jl,n} \right) $$,$$h_{jl,n} \in H$$
を導入する.すなわち,元$$h_{jl,n}g_{n}$$ と元$$g_{n}$$とを$$h_{jl,n}$$を法として合同と見ると,
還元積に関して,系$$\left\{ g_{1},g_{2}, \ldots ,g_{s} \right\} $$ は閉じている.つまり,$$H$$を法とする群$$ G(\textrm{mod}H ) $$を作っている.
剰余類の代表系への,すべての我々の要請は,法による(modulus)群の概念に統合される.正規の拡大の存在条件は,次のような形にまとめることができる.《群$$H \vartriangleleft G$$の拡大$$G$$は,もし剰余類の代表元の組が,商群$$G/H$$に同型な$$H$$を法とする群$$G(\textrm{mod}H)$$を作るならば,存在する.》 組$$\left\{ g_{1},g_{2}, \ldots ,g_{s} \right\} $$ の同値性の問題は,対応する群の同型の問題に帰着する.積の法則が違うために,群$$G(\textrm{mod}H) $$は一般には$$G$$ の部分群ではない.特に,もし,全係数が$$h_{jl,n} \equiv h_{1}$$ となるような,代表系を選ぶことができるなら,法による群は,普通の群$$G^{*}=\left\{ g_{1},g_{2}, \ldots ,g_{s} \right\} $$ ($$G$$ の部分群)になる.群$$G$$は,このとき共型(symmorphic)と呼ばれる.もしそのような選択が不可能なときは,群$$G$$は非共型(nonsymmorphic)である.拡大$$G$$は群$$H$$ と群$$G(\textrm{mod}H)$$の《積》として作ることができる.全元$$h_{1},h_{2}, \ldots ,h_{m} \in H$$ を1つづつ元$$g_{1},g_{2}, \ldots ,g_{s} \in G(\textrm{mod}H)$$ に乗じて集めると集合$$G$$ が得られる:
$$G=\left\{ h_{1}g_{1},h_{2}g_{1}, \ldots ,h_{m}g_{1},h_{1}g_{2},h_{2}g_{2}, \ldots ,h_{m}g_{2},h_{1}g_{s},h_{2}g_{s}, \ldots ,h_{m}g_{s} \right\} $$ (4)
拡大を作るために利用した群において,唯一の共通元は
$$H \cap G(\textrm{mod}H)=h_{1}=g_{1}=e \in G$$ であることを思い出そう. $$G(\textrm{mod}H)$$ は$$G$$の部分群ではないので,拡大(4)を条件積と呼び次の記号を用いることにする.
$$G=H \bullet G(\textrm{mod}H), H \vartriangleleft G, G(\textrm{mod}H) \not\subset G, H \cap G(\textrm{mod}H)=e \in G$$ (5)
共型(symmorphic)群$$G$$に対しては,条件積(5)は法による群を普通の群
$$G^{*}=\left\{ g_{1},g_{2}, \ldots ,g_{s} \right\} $$ ($$G$$の正規あるいは非正規な部分群)に入れ換えることにより作られ,さらに簡単な直積あるいは半直積となる.
2つの群の直積 $$G=H \otimes G^{*}, H \vartriangleleft G, G^{*} \vartriangleleft G, H \cap G^{*}=e \in G$$は,2連元$$h_{i}g_{j} \in G$$ に対する次の積則から定義される:
$$h_{i}g_{j} \otimes h_{k}g_{l}=h_{i}h_{k}g_{j}g_{l}$$,$$h_{i}h_{k} \in H$$, $$g_{j} , g_{l} \in G^{*}$$ (6)
半直積$$G=H \bullet G^{*}, H \vartriangleleft G, G^{*} \vartriangleleft G, H \cap G^{*}$$ は,積則:
$$h_{i}g_{j} \bullet h_{k}g_{l}=h_{i}h_{k}^{g_{j } }g_{j}g_{l} , h_{i}h_{k}^{g_{j } }=g_{j}h_{k}g_{j}^{-1} \in H , g_{j} , g_{l} \in G^{*}$$ (7)
で定義される.直積は(6)で,任意の2つの群$$H$$と$$G^{*}$$に対して完全に定義される;半直積は(7)に従い自己同型変換$$g_{j}h_{k}g_{j}^{-1}h_{f}$$ (すべての$$h_{k} \in H, g_{j} \in G^{*}$$ に対して)を求める問題として定義される.一般に,(5)-(7)のすべての場合にわたって,$$G(\textrm{mod}H)$$あるいは$$G^{*}$$は$$H$$に対して自己同型群である($$H \vartriangleleft G$$ を保つ:任意の$$h_{k} \in H, g_{j} \in G$$に対して $$g_{j}Hg_{j}^{-1} \in H$$).$$G^{*}$$の元を$$h_{1}g_{j} , h_{1}g_{l}$$の型で表すと,積則(6),(7)は部分群$$G^{*} \subset G$$ 内で積の閉性が保存されていることを確認できる: $$h_{1}g_{j} \cdot h_{1}g_{j}=h_{1}g_{j}g_{l}$$ なぜなら$$h_{1}^{g_{j } }=g_{j}h_{1}g_{j}^{-1} \equiv h_{1}$$
非共型(nonsymmorphic)群$$G$$は,元$$g_{j} \in G^{*}$$の部分を次のような新しい元で置き換えることにより,直積,半直積の型に作れる: $$g_{j}^{H}=\alpha _{j}g_{j} \equiv g_{j}(\textrm{mod}\alpha _{j})$$
$$g_{1}^{H}=\alpha _{1}g_{1} \equiv g_{1}(\textrm{mod}\alpha _{1}), g_{2}^{H}=\alpha _{2}g_{2} \equiv g_{2}(\textrm{mod}\alpha _{2}), \ldots , g_{s}^{H}=\alpha _{s}g_{s} \equiv g_{s}(\textrm{mod}\alpha _{s})$$ (8)
一般に,$$\alpha _{1} \equiv h_{1}$$であるが,合同式の法となる第1系の残りの係数は$$\alpha _{j} \notin H$$である.しかしながら,$$m$$を元$$g_{j}$$の位数とするとき,$$\left( \alpha _{j}g_{j} \right) ^{m}=\alpha _{j}^{m}g_{j}^{m}=h_{1}g_{1}, \alpha _{j}^{m}=h_{1} \in H$$となる. (8)の置き換えで,群$$G^{*}$$はすでに学んだ還元積による$$H$$を法とする同型な群$$G^{H}=\left\{ g_{1}^{H},g_{2}^{H}, \ldots ,g_{s}^{H} \right\} $$に変る*.
-------------------------------------------------------------
*非共型(nonsymmmorphic)拡大$G$を得るための法による(modulus)群$$G(\textrm{mod}H)$$を$$G^{H}$$と記す.
-------------------------------------------------------------
$$g_{j}^{H}g_{l}^{H}=h_{jl,n}g_{n}^{H} \equiv g_{n}^{H}(\textrm{mod}h_{jl,n})$$, $$h_{jl,n} \in H, g_{n}^{H} \in G^{H}$$ (9)
あるいは,直積と半直積にそれぞれ対応して
$$\left( \alpha _{j}g_{j} \right) \left( \alpha _{l}g_{l} \right) =\alpha _{j}\alpha _{l}g_{j}g_{l}=\alpha _{j}\alpha _{l}\alpha _{n}^{-1}\left( \alpha _{n}g_{n} \right) \equiv \left( \alpha _{n}g_{n} \right) \left( \textrm{mod}h_{jl,n} \right) $$ (9a)
$$\left( \alpha _{j}g_{j} \right) \left( \alpha _{l}g_{l} \right) =\alpha _{j}\alpha _{l}^{g_{j } }g_{j}g_{l}=\alpha _{j}\alpha _{l}^{g_{j } }\alpha _{n}^{-1}\left( \alpha _{n}g_{n} \right) \equiv \left( \alpha _{n}g_{n} \right) \left( \textrm{mod}h_{jl,n} \right) $$ (9b)
(9a)と(9b)から,合同式の法となる第2の係数系が求まる:
$$h_{jl,n}=\alpha _{j}\alpha _{l}\alpha _{n}^{-1}$$ および $$h_{jl,n}=\alpha _{j}\alpha _{l}^{g_{j } }\alpha _{n}^{-1}$$
ここで,$$\alpha _{j}^{g_{j } }=g_{j}\alpha _{l}g_{j}^{-1}=\alpha _{k}$$は,$$\alpha _{j}$$の自己同型共役元(automorphism transformations of the moduli)であり,$$\alpha _{k}g_{k}=g_{k}^{H} \in G^{H}$$, $$\alpha _{j}^{g_{j } }=\alpha _{j}$$ (定義から)となる.
群$$G^{H}$$において単位元の役割は元$$g_{1}^{H}=h_{1}g_{1}$$が果たす.逆元は,それぞれ,
$$\left( \alpha _{j}g_{j} \right) ^{-1}=\alpha _{j}^{-1}g_{j}^{-1}$$ および $$\left( \alpha _{j}g_{j} \right) ^{-1}=\left( \alpha _{j}^{-1} \right) ^{g_{j}^{-1 } }g_{j}^{-1}$$
量$$\alpha _{j}$$の系は,それ自身で,群$$G^{H}=\left\{ g_{1}^{H},g_{2}^{H}, \ldots ,g_{s}^{H} \right\} $$と同型な,$$h_{jl,n}$$を法とする群$$A^{H}=\left\{ \alpha _{1},\alpha _{2}, \ldots ,\alpha _{s} \right\} $$をつくることに注意しよう.元間の対応は: $$\alpha _{j} \longleftrightarrow g_{j}^{H}$$, $$\alpha _{l} \longleftrightarrow g_{l}^{H}$$および, $$\alpha _{j}\alpha _{l}=h_{jl,n}\alpha _{n} \equiv \alpha _{n}(\textrm{mod}h_{jl,n}) \longleftrightarrow g_{j}^{H}(\textrm{mod}h_{jl,n}) \equiv h_{jl,n}g_{n}^{H}=g_{j}^{H}g_{l}^{H}$$
これから,上記の式で用いた逆元記号が正当であるとわかる: $$\alpha _{j}\alpha _{j}^{-1}=\alpha _{j}^{-1}\alpha _{j}=\alpha _{1}=h_{1}$$
対応 $$g_{j}^{H}g_{l}^{H}=h_{jl,n}g_{n}^{H} \equiv g_{n}^{H}\left( \textrm{mod}h_{jl,n} \right) \longleftrightarrow g_{n}=g_{j}g_{l} \longleftrightarrow Hg_{n}=Hg_{j}g_{l}$$から導かれる群$$G^{H} \longleftrightarrow G^{*} \longleftrightarrow G/H$$の同型は,非共型(nonsymmorphic)拡大の存在を保証する.
非共型(nonsymmorphic)群を,2つの群の条件積(準積:условное произведениеquasi-product)で作ろう:
$$G=H \bigcirc G^{H}=$$
$$=\left\{ h_{1}\left( \alpha _{1}g_{1} \right) ,h_{2}\left( \alpha _{1}g_{1} \right) , \ldots ,h_{m}\left( \alpha _{1}g_{1} \right) , \ldots ,h_{1}\left( \alpha _{s}g_{s} \right) ,h_{2}\left( \alpha _{s}g_{s} \right) , \ldots ,h_{m}\left( \alpha _{s}g_{s} \right) \right\} $$ (10)
このとき条件直積(準直積:прямыхquasi-direct)$$ \odot $$と条件半直積(準半直積:полупрямых условных произведенийquasi-semidirect)$$ \bigcirc $$を区別して:
$$h_{i}\left( \alpha _{j}g_{j} \right) \odot h_{k}\left( \alpha _{l}g_{l} \right) =h_{i}h_{k}\left( \alpha _{j}g_{j} \right) \left( \alpha _{l}g_{l} \right) =h_{i}h_{k}h_{jl,n}\left( \alpha _{n}g_{n} \right) $$
$$h_{jl,n}=\alpha _{j}\alpha _{l}\alpha _{n}^{-1} \in H$$ (11)
$$h_{i}\left( \alpha _{j}g_{j} \right) \bigcirc h_{k}\left( \alpha _{l}g_{l} \right) =h_{i}h_{k}^{\left( \alpha _{j}g_{j} \right) }\left( \alpha _{j}g_{j} \right) \left( \alpha _{l}g_{l} \right) =h_{i}h_{k}^{\left( \alpha _{j}g_{j} \right) }h_{jl,n}\left( \alpha _{n}g_{n} \right) $$ (12)
ここで,$$h_{jl,n}=\alpha _{j}\alpha _{l}^{g_{j } }\alpha _{n}^{-1} \in H$$
$$h_{k}^{\left( \alpha _{j}g_{j} \right) }=\left( \alpha _{j}g_{j} \right) h_{k}\left( \alpha _{j}g_{j} \right) ^{-1}=h_{f} \in H$$ for all $$h_{k} \in H, \left( \alpha _{j}g_{j} \right) \in G^{H}$$
(11),(12)と(6),(7)を比較し,共型(symmorphic)群(4)のモデルから作られた非共型(nonsymmorphic)群(10)は,それと同型でないことがわかる.これは積則(11),(12)の中に同型を破る量$$h_{jl,n}$$が現れるからである†.
---------------------------------------------------------
†英語版注] (4)と(10)による群は,式(11),(12)で$$h_{jl,n} \equiv h_{1}\left( \textrm{mod}h_{jl,n} \right) $$なら,同型である.
---------------------------------------------------------
与えられた共型(symmorphic)群に関して,非共型(nonsymmorphic)群を実際に作ることは,法となる係数(congruence moduli)の第1系と第2系を決定することに帰着する(p207の文献).あまり大きくない位数の群$$G^{H}$$に対しては,もし同型群$$G^{*}$$の乗積表がわかっていて,$$\alpha _{j}$$が決まっているなら,係数$$h_{jl,n}$$の表は目の子選択で簡単に求めることができる.
表挿入
$$ \begin{array}{c|ccccc} G^{*} & g_{1} & \cdots & g_{l} & \cdots & g_{s} \\[0mm] \hline g_{1} & g_{1} & \cdots & g_{l} & \cdots & g_{s} \\[0mm] \vdots & \vdots & & \vdots & & \vdots \\[0mm] g_{j} & g_{j} & \cdots & g_{n} & \cdots & g_{p} \\[0mm] \vdots & \vdots & & \vdots & & \vdots \\[0mm] g_{s} & g_{s} & \cdots & g_{q} & \cdots & g_{r} \end{array}$$ $$\longrightarrow$$ $$\begin{array}{c|ccccc} h_{jl,n} & g_{1}^{H} & \cdots & g_{l}^{H} & \cdots & g_{s}^{H} \\[0mm] \hline g_{1}^{H} & h_{1} & \cdots & h_{1} & \cdots & h_{1} \\[0mm] \vdots & \vdots & & \vdots & & \vdots \\[0mm] g_{j}^{H} & h_{1} & \cdots & h_{jl,n} & \cdots & h_{js,p} \\[0mm] \vdots & \vdots & & \vdots & & \vdots \\[0mm] g_{s}^{H} & h_{1} & \cdots & h_{sl,q} & \cdots & h_{ss,r} \end{array} $$
表中に$$h_{1}$$が現れるのは,単位元への《法係数のない》積の結果である:
$$\left( \alpha _{j}g_{j} \right) \left( h_{1}g_{1} \right) =h_{j1,j} \times \left( \alpha _{j}g_{j} \right) =\left( \alpha _{j}g_{j} \right) $$, $$\left( h_{1}g_{1} \right) \left( \alpha _{j}g_{j} \right) =h_{1j,j}=\left( \alpha _{j}g_{j} \right) $$,
ただし,$$h_{j1,j}=h_{1j,j}=h_{1}$$,$$j=1,2, \ldots ,s$$
量$$h_{1}$$は,表中で,《係数のない》元$$g_{i}^{H} \equiv g_{i}$$, $$g_{k}^{H} \equiv g_{k}$$(このような元は全部で単位元$$g_{1}^{H} \equiv g_{1}$$とともに群$$G^{*}$$の部分群$$G_{1}^{*}$$を作る)の積に対応する行と列の交点に現れる.
表14挿入
表 14 回転群の拡大としての結晶点群
$$ \begin{array}{ccc} \hline 回転群 & 反転群 & 鏡映群 \\[0mm] \hline 1 & \bar{1}=1 \otimes \bar{1} & m=1 \otimes m \\[0mm] 2 & 2/m=2 \otimes \bar{1} & mm2=2 \otimes m \\[0mm] 3 & \bar{3}=3 \otimes \bar{1} & \bar{6}=3 \otimes m \\[0mm] - & - & 3m=3 \ominus m \\[0mm] 4=2 \odot 4\left( \textrm{mod}2 \right) & 4/m=4 \otimes \bar{1} & \bar{4}=2 \odot \bar{4}\left( \textrm{mod}2 \right) \\[0mm] - & - & 4mm=4 \ominus m \\[0mm] 6=3 \otimes 2 & 6/m=6 \otimes \bar{1} & 6mm=6 \ominus m \\[0mm] 222=2 \otimes 2 & mmm=222 \otimes \bar{1} & \bar{4}2m=222 \ominus m \\[0mm] 32=3 \otimes 2 & \bar{3}m=32 \otimes \bar{1} & \bar{6}m2=32 \otimes m \\[0mm] 422=4 \ominus 2=222 \ominus 2 & 4/mmm=422 \otimes \bar{1} & - \\[0mm] 622=6 \ominus 2=32 \otimes 2 & 6/mmm=622 \otimes \bar{1} & - \\[0mm] 23=222 \otimes 3 & m\bar{3}=23 \otimes \bar{1} & \bar{4}3m=23 \ominus m \\[0mm] 432=23 \ominus 2 & m\bar{3}m=432 \otimes \bar{1} & - \\[0mm] \hline \end{array} $$
(注意) 反転群でもなく対称心をもたない群は,鏡映群に分類した.
非正規拡大(noninvariant extensions реинвариантных расширений)の理論を残したが,32結晶群を回転群の拡大とみなし,直積,半直積,条件積への分解表を導いた.表14は全結晶群が8つの生成群の対の積によつて得られることを示している.
$$H=1,2,3, G^{*}=2,m,\overline{1}, G^{H}=4(\textrm{mod}2), \overline{4}(\textrm{mod}2)$$
これらのうち,法による群は次の乗積表で定義される.
$$ \begin{array}{c|cc} 4(\textrm{mod}2) & \texttt{1} & 4^{H} \\[0mm] \hline \texttt{1} & \texttt{1} & 4^{H} \\[0mm] 4^{H} & 4^{H} & 2 \equiv 1(\textrm{mod}2) \end{array} $$
$$ \begin{array}{c|cc} \overline{4}(\textrm{mod}2) & \texttt{1} & \overline{4}^{H} \\[0mm] \hline \texttt{1} & \texttt{1} & \overline{4}^{H} \\[0mm] \overline{4}^{H} & \overline{4}^{H} & 2 \equiv 1(\textrm{mod}2) \end{array} $$
これらの群($$4^{H}=4^{-1}2$$ と $$\overline{4}^{H}=4\overline{1}$$)の元$$g_{j}^{H}=\alpha _{j}g_{j}$$の積は,(9a)に従う:
$$\left( 4^{-1}2 \right) \left( 4^{-1}2 \right) =4^{-1}4^{-1}22=21 \equiv 1\left( \textrm{mod}2 \right) , \left( 4\overline{1} \right) \left( 4\overline{1} \right) =44\overline{1}\overline{1}=21 \equiv 1\left( \textrm{mod}2 \right) $$
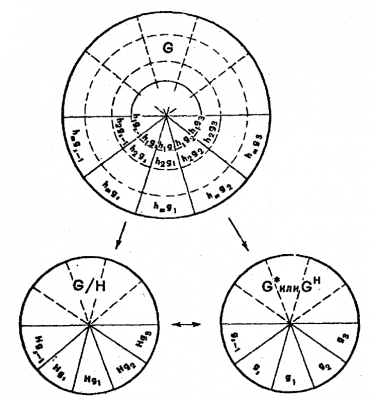
更なる例を後に見ることになるが,生成群間の積の方法は,新しい群を導く効果的な手段であることがわかる.この節を終えるにあたり,もとの群と最後の群を結び付けている準同型および同型対応の図と正規拡大を得る道筋をを辿ってみよう(図204).
図204挿入
図204.
正規(不変)拡大の説明図に見られる群の間の準同型($$ \to $$)と同型($$ \leftrightarrow $$).
説明図$$G^{*} \leftrightarrow G/H \gets G$$に従い,任意の群$$G^{*}=\left\{ g_{1},g_{2}, \ldots ,g_{s} \right\} $$を商群
$$G/H=\left\{ Hg_{1},Hg_{2}, \ldots ,Hg_{s} \right\} $$のモデルとして選び,$$H=\left\{ h_{1},h_{2}, \ldots ,h_{m} \right\} $$を準同型
$$G^{*} \gets G$$の核($$H$$は$$G$$の部分群で恒等元$$g_{1} \in G^{*}$$の上に写像される)として,共型拡大$$G=G \otimes G^{*}$$あるいは非共型拡大$$G=H \ominus G^{*}$$を作る.$$G/H$$において,元$$Hg_{i}$$を元の集合$$\left\{ h_{1}g_{i},h_{2}g_{i}, \ldots ,h_{m}g_{i} \right\} $$で置き換え,求める拡大$$G$$を得る:
$$ \left\{h_{1}g_{1}, \ldots ,h_{m}g_{1}, \ldots ,h_{1}g_{s}, \ldots ,h_{m}g_{s}\right\} $$
$$ \swarrow \searrow $$ (4)
$$ \left\{Hg_{1},Hg_{2}, \ldots ,Hg_{s}\right\}$$ $$\leftrightarrow$$ $$\left\{g_{1},g_{2}, \ldots g_{s}\right\} $$
ここで,群の間に必要な対応があることは,以下の写像:
$$h_{i}g_{j}\left( i=1,2, \ldots ,m \right) \to Hg_{j} \leftrightarrow g_{j}\left( j=1,2, \ldots g_{s} \right) $$
および,群$$G$$に対する積則(6),(7),$$G/H$$に対する積則(3)により確かめられる.
非共型群$$G=H \odot G^{H}$$または$$G=H \bigcirc G^{H}$$は,
置換$$G^{*} \longleftrightarrow G^{H}=G_{1}^{*}g_{i} \cup G_{1}^{*}g_{i+1}^{H} \cup \ldots \cup G_{1}^{*}g_{i+p}^{H}$$により得られ,$$G_{1}^{*}=\left\{ g_{1},g_{2}, \ldots ,g_{i} \right\} $$は群$$G^{*}$$と$$G^{H}$$の共通部分群,元$$g_{i+1}^{H}=\alpha _{i+1}g_{i+1}, \ldots ,g_{i+p}^{H}=\alpha _{i+p}g_{i+p}$$, $$p + i=s/i$$は部分群$$G_{1}^{*}$$の指数(法による群$$G^{H}$$の$$G_{1}^{*}$$に関する展開における)である.置換$$G^{*} \longleftrightarrow G^{H}$$は,共型群(4)を非共型群(10)に,積則(6),(7)を(11),(12)に換える.ダイヤグラム中で,群$$G^{*}$$と$$G^{H}$$の元は同じ記号$$h_{i}g_{j}$$で標記する:元の間の対応は$$h_{i}g_{j} \longrightarrow Hg_{j} \longleftrightarrow g_{j}$$同様に標記される円のセクター間の対応に反映される.$$g_{1}=h_{1}=e$$であるので,群$$\overline{G}^{*}=\left\{ h_{1}g_{1},h_{1}g_{2}, \ldots ,h_{1}g_{s} \right\} $$は,$$G^{*}$$と同一で群$$\overline{H}=\left\{ h_{1}g_{1},h_{2}g_{1}, \ldots ,h_{m}g_{1} \right\} $$は$$H$$と同一である.