
数学月間の会SGKのURLは,https://sgk2005.org/ になりました.


数学月間の会SGKのURLは,https://sgk2005.org/ になりました.
Fig.1の円盤内部は双曲幾何の支配する世界で,ポアンカレの円盤モデルと呼ばれます.
この円盤世界の直線は,円盤の縁に直交する円弧です.もちろん,円盤の中心を通る直線は円盤の縁で直交するので,この円盤世界でも直線です.
この円盤世界は,正7角形のタイルが頂点で3つ集まるように敷き詰められています[双曲面の正則分割{7,3}].正7角形の辺は,この双曲世界の直線でできています.
直線に沿って円盤の縁に向かって進んだとすると,自分の世界もどんどん小さくなり縁に到達するには無限の時間がかかるようになっている世界です.
{7,3}分割の正7角形のタイルは,円盤の縁に近づくにつれどんどん小さくなっていますが,円盤の中にいる人にとっては全部同じ大きさ(言葉をかえれば円盤内は無限に広い)です.
Fig.1 Fig.2
コクセター万華鏡は,正7角形タイルの中を14個の直角3角形(7,3,2)に分割してできます.この直角3角形の頂点の角度は(π/7,π/3,π/2)ですから,直角3角形(7,3,2)と略記しました.
この直角3角形を鏡室にして作った万華鏡をコクセター万華鏡と呼ぶことにしました.
それは,同様な分割{6,4}の論文をコクセターがエッシャーに送って,それがエッシャーの極限としての円の作品を生んだからです.
{7,3}分割を直角3角形(7,3,2)のコクセター万華鏡にすると,Fig.2のように3角形のどの頂点周りにも偶数の直角3角形が集まるので,円盤内の世界全体が市松模様になります.
円弧の1つを円柱鏡にして,この円弧で分けられた左世界の像を映し出した実験をした撮影してみましたFig.3.右世界の像は左の世界の鏡像なので,円柱鏡を境として市松模様が逆転しているのがわかるでしょう.
Fig.3
円柱鏡(円の内側で反射)の焦点は収差のため,このような曲線になります.
このような反射光線のが作る包絡線の形を“火線”といいます.
この曲線の形はネフロイド(サイクロイドの仲間)と呼ばれます.
■コクセター万華鏡
このコクセター万華鏡は直角3角形(7,3,2)の辺を鏡にして作られます.
この双曲幾何のポアンカレ円盤世界の直線は,円盤の縁で直交する円弧です.
双曲面の正則分割{7,3}の正7角形を,直角3角形(7,3,2)で細分したコクセター万華鏡を示します.
この万華鏡像は,
直角3角形(7,3,2)の辺を鏡にして,円による反転(数学的演算)により得られます.
しかしながら,円柱鏡による反射像には収差があるので,反射を繰り返すとボケてしまいます.
円柱鏡の1回反射の実験例を示します.右側世界は左側世界の鏡像なので,市松模様が鏡面に沿ってずれているのがわかるでしょう.
■風が吹けば桶屋が儲かるバタフライ効果
バタフライ効果とは,気象学者のエドワード・ローレンツが1972年にアメリカ科学振興協会で行った講演のタイトル”予測可能性:ブラジルの1匹の蝶の羽ばたきはテキサスで竜巻を引き起こすか?”に由来します.
複雑系では,単純な因果列ではなく,あらゆる原因がどの結果にも反映されるので,予測できない結果をもたらす可能性があることを言います.
□定まっているようで定まらない運命
系の運動を記述する方程式は正しく作れるのだが,この方程式の解析解が求まる(可積分)とは限りません.現実は,非可積分の場合がほとんどで,教科書で習う可積分の場合は例外的幸運な場合です.1880年代にポアンカレは,ニュートンの運動方程式ですべての運動が定まっているはずの世界で,三体問題は解析解が得られないことを証明しました.
□非可積分の世界とバタフライ効果
非可積分の方程式の解は,コンピュータによる数値計算で求めることができます.しかし,このような系の解では,方程式のパラメータや初期値によって,解が分岐したりカオスと呼ばれる定まらない状態になったりします.
このような状態は,ロジスティク写像の漸化式Xn+1=aXn(1-Xn) や同様な漸化式 Xn+1=Xn2+λ でも見られます.ここで得られる実数列 Xn(n→∞)が,実数パラメータλやaの値により,振動したり発散したり,定まらない状態になったりすることが起こります.また,初期値のごくわずかのずれが,Xnの劇的な変化を生むことがあります.これがバタフライ効果と呼ばれる所以です.
■マンデルブロの登場とフラクタル
IBMトーマス・J・ワトソン研究所にいたマンデルブロは,綿花などの価格変動を調べていて,不規則な変動データの中に隠れている自己相似性を見つけフラクタルとなずけました.フラクタル幾何学は1982年に発表されました.
マンデルブロ集合(奇妙なフラクタル構造)と言うのは,
f(z) = z2 + Cという写像で生まれる複素数列を,
初期値z0 = 0として,z1 = f(z0), z2 = f(z1), …とくり返し計算し,n → ∞で|zn|が発散しないような,複素平面上の複素数Cの集合「初項z0 = 0に対して,発散しないCは何か」のことです.
マンデルブロ集合の境界(数列が発散する/しないの限界)ではカオスの発生があり,美しく不思議に入り乱れたフラクタルが見られます.
Fig.1
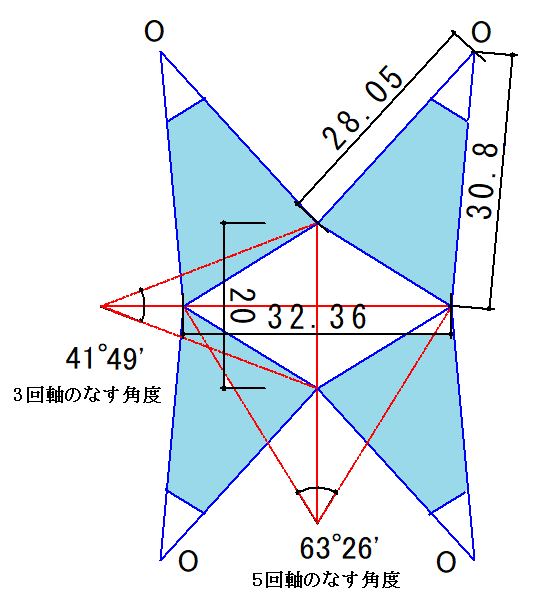
菱形30面体と12・20面体とは互いに双対な多面体です.双対の説明はFig1に図示しました.さらに,12・20面体は互いに双対な正12面体と正20面体とを重ねたときの共通部分でもあります.
注)Fig.1の重な合わせでは,共通部分はサッカーボール[5,6,6]の半正多面体ですが,正20面体のを少しづつ大きくしていくと,[5,3,5,3]の半正多面体(12・20面体)になる点があります.
菱形30面体の頂点は,正12面体の頂点(3回軸の位置)と正20面体の頂点(5回軸の位置)とから構成されています.菱形面の短対角線(正12面体の正5角形面の辺長)をaとし,長対角線(正20面体の正3角形面の辺長)をbとすると,a:b=1:Φ=2:1+√5 の黄金比です.正12面体の頂点のうちの8個を使い,一辺Φaの立方体を内接できるので,正12面体の外接球の半径は,R12=√3Φa/2です.
一方,正20面体の外接球の半径は,R20=(b/4)√(10+2√5)です.
寸法をa=2,b=1+√5,Φ=1.618にすると,R12=2.80,R20=3.08が得られます.
実際の製作は展開図に記入した寸法(10倍)にすると作り易いです.
ミラー紙(厚さ0.25mm程度の厚紙)を使って,展開図の鏡を作りピラミッド(内側が鏡)のような形に組み立てます.O点は立体(ピラミッド)の中心に相当し,O点の周囲は光の窓になります.覗くのは菱形面(ピラミッドの底面)の外部からです.
針金で正4面体ABCDを作り,持ち手をつけて,正4面体をシャボン液の中に浸してからゆっくり引き上げると,どのような面にシャボン膜ができるでしょうか?
実験してみてください.針金枠の正4面体の面にシャボン膜ができると思いますか?
多分,正4面体の中心Oと正4面体の辺でできる三角形,例えば,△OABなどの膜ができると思います.正4面体は辺が6個ありますから,このような膜は6枚あります.
Oから正4面体の各頂点へ,線分OA,OB,OC,ODの4本がありこの線分が3つのシャボン膜の境界になります.
(1)Oから正4面体の各頂点に向かう線分同士のなす角度は何度でしょうか?
(2)△OABのような6つの膜が1点で出会うOのような点が必ずできるでしょうか?
(3)正4面体の4つの面の面積合計と,△OABの面積x6とでどちらが大きいでしょうか?
(4)どのようなシャボン膜の形のつり合いが実現するでしょうか?
色々な疑問が起こり難しい問題です.実験してみて推測してみましょう.
針金の枠が立方体のときは,どのような膜の形になるでしょうか?
実験してみると下図のような膜ができると思います.
このような膜の形ができることを説明してください.
1976年,ドイツのRegensburg大学のKurt Fischerは,神経の生理学モデルを研究し,フィボナッチ数の発生をここでも発見した[177].神経繊維に沿って移動するインパルスは,ナトリウムまたはカリウムのイオンに由来し,n>=2の細胞からなる同一の膜貫通孔を通って流れる.微量のカルシウムイオンCa2+が孔に入ると,孔内のナトリウムイオンNa+の流れを止めることができる.
これらのイオンは,細孔の入り口を除いて,それぞれ1つまたは2つの細胞を占有することができ,これらの2つの状態をそれぞれ1あるいは2と標記する.図3.39は典型的な孔の状態で,0と表示したのは空の細胞である.
ナトリウムは,孔のいずれの端でも出入りすることができるが,カルシウムは孔の左側でのみ出入りできると仮定する.その結果,孔内のカルシウムイオンは,この孔を通るナトリウムの流れを妨げる.
ロシアの数学者Andrey Andreyevich Markov (1856-1922)にちなんで名付けられたこのマルコフ確率過程は,ツリー構造で表すことができる.木の頂点は細孔の可能な状態を表し,そのエッジは状態間の可能な遷移を表す.たとえば,図3.40に,5つの空でない細胞を有する孔の様々な可能な状態を示す.
図3.40
ツリーは2種類の頂点で構成されていることに注意せよ.すなわち,右端のセルに1,あるいは,右の2つのセルの中央に2があるものだ. レベル5のすべての状態は後者で,状態の右側にカルシウムが存在するため,ナトリウムイオンの右への移動がもはや実行可能ではない.図3.41に図3.40のツリー骨格が描かれている.これは図2.1のフィボナッチツリーに非常に似ている.いずれの図からも,5つの空でない細胞を有する孔は,レベル5に5=F5個の状態を有することがわかる.
図3.41
一般的に,n個の空でない細胞を有する孔は,レベルnにFn個の状態を有する.これは,レベルnの状態数がフィボナッチ再帰関係を満たすことからわかる.
1963年,カリフォルニア州サンノゼにあるサンノゼ州立大学のS.L. Basinは,”電気ネットワークに関心のある人々まで,我が友フィボナッチから逃れることはできない”[23]と書いた.ここでは,フィボナッチ数が電気ネットワークの研究にどのように現れるか示そう.
今年の桜
■NPO法人「数学月間の会(SGK)」(理事長岡本和夫)が設立されました.
詳細は新ウエブサイト http://sgk2005.saloon.jp/ をご覧ください.
数学月間の会の会員募集中です.ご支援のほどよろしくお願いします.
問い合わせや会員登録は sgktani@gmail.com
■数学月間の会とは
数学はあらゆる文化・学術の基盤で,科学,工学,産業,芸術,医学,経済など,社会のあらゆる分野を数学が支えています.しかしながら,一般市民,特に,生徒・学生とその両親は,数学学習を敬遠する風潮にあり,これが数学力の低下をもたらしています.
米国では,1986年4月17日のレーガン宣言により国家的な行事として「数学月間」MAMが開始され,今日に至ります.米国MAMは,数学系の学協会が参加するJPBM(Joint Policy Boad for Maths)が,毎年,社会を反映した数学テーマを選定し,毎年4月に種々の数学イベントを展開し,国民からの事後評価も受けます.皆が知りたい時局の数学を,種々のレベルで学習できるウエブサイトができ,そこにエッセイや論文が集積され,そのテーマの数学を基礎から最先端まで,学生が独習できる優れたガイドになります.MAM期間には,一般から専門家まで,小学生から大学生まで,いろいろなレベルのイベントが全国で展開されます.米国が国家的行事のMAMを決断した背景には,国民の数学力が低下し,米国の産業力も低下するとの焦りがありました.日本も同様な状況にあるものの,国家的行事の数学月間は実施されておりません.
近年,日本でもSTEM(科学・技術芸術・工学・数学)教育が叫ばれていますが,これも2003年に始まった米国のSTEM教育に源を発します.これらの科目の中で統合的に数学を教える試みは良いことですがまだ成功していません.数学月間の視点はSTEM教育へも貢献できるものと思います.
数学を学ぶ同好会,塾,講習会,講演会などは種々あります.これらも重要であるのは言うまでもありませんが,我々の目指す「数学月間」活動は,このような数学同好者の内部にとどまる活動ではありません.数学がかかわるあらゆる分野を横断して数学を紹介する数学外の一般市民に向けた活動です.
一般市民,学生,生徒に対し,数学が社会を支えている事例を,わかり易く啓蒙する事業を行い,数学への社会的共感を獲得し,社会に数学文化を普及させ,社会の発展に寄与することを目的とする市民の活動です.どうぞ活動にご協力ください.
日本の数学月間は,2005年に日本数学協会が7/22-8/22を数学月間と定めたことに始まります.任意団体「数学月間の会(代表;故片瀬豊)」は,2005年の発足以来,ボランティア・ベースながら,毎年,数学月間の初日7/22に,数学月間懇話会を開催し,計37件の啓蒙的な講演を一般市民に対し実施することで,数学啓蒙活動をこの時期に集中し,数学の重要性を社会にアピールしてきました.このような数学月間活動は,米国MAMのように国家的行事として行うべき性質のもので,個人寄付金とボランティア・ベースで行う現状には限界があります.数学同好会ではなく,活動を社会に波及させるためには,NPO法人格を得た「数学月間の会」が,数学の内部にとどまらず社会の諸分野に横断的に呼びかけ活動し,「社会と数学の架け橋」になることが必要でした.
4月から新しい「数学月間の会」の会員になり,一緒に活動しませんか.
━━━━━━━━━━━━━━━━━━━━
数学月間SGK通信 [2019.03.26] No.260
<<数学と社会の架け橋=数学月間>>
━━━━━━━━━━━━━━━━━━━━
周期的な2次元平面の互いに独立な並進ベクトルは2方向とれます.
これら2本の並進ベクトルが挟む平行4辺形を単位胞といいます.
並進ベクトルの組み(単位胞の形)を対称性で分類したものがブラベー格子です.
2次元のブラベー格子には,図に示す5種類があります.
そして,それぞれに対応する格子の図も掲載しておきました.
さて,以下に伝統文様を10種挙げました
図の中に赤色ベクトルで,並進の周期を書き込んだ図もあります.
1.書き込んでない図にも赤色ベクトルを書き込んでみましょう.
赤色ベクトルの選び方はいろいろ可能ですが,
単位胞の形(赤色ベクトルで囲まれた平行4辺形)が
A正方形,B長方形,C120°の菱形,D任意角度の菱形,
の4種類のどれかにあてはめるようにとれます.
2次元のブラベー格子の5種類のうち,一般形の平行4辺形に属する伝統文様は,
ここの例には挙げていません.
2.それぞれの伝統文様は,A,B,C,Dのどのタイプに属するでしょうか.
3.伝統文様のいくつかを,どこかで見たことがあるでしょうか.
私は立涌を壁紙で見かけます.
■ 円に点Bを通る2直線が交差しているときに,方冪の定理が成り立ちます.
■2つの長さの加法,減法は簡単です.以下の図をご覧ください:
■結局,直線定規とコンパスだけを有限回繰り返し用いて作図できる長さは
加法,減法,乗法,除法,開平です.
開平を繰り返せは,2のべき乗根(4乗根,8乗根,...)は作図できますが,
例えば,立方根は作図できません(この証明は難かしいのでスキップ).