1.結晶空間群.結晶点群
結晶は周期的な内部構造を持ちます.周期的な離散空間を<結晶空間>と言い,
その対称性は<結晶空間群>で記述します.結晶空間群の種類は,3次元では230種類です.
3次元の周期構造の幾何学的な表現を<格子>と言ったり,その数学的な表現を<並進群>と言ったりします.
結晶空間の中で,格子分だけ移動しても,周囲の状況は移動する前の状況と全く同じなので,無限に繰り返す結晶の中で自分がどこにいるか区別できません.そこで,格子分だけ移動した点はすべて同値とみなして,
無限に広い結晶空間を1つの単位胞の中に畳み込んでしまうことができます.
あたかも,無限に続く時間を,時計の文字盤(12時間)に畳み込んでしまうのと同じです.
<単位胞>(有限図形)の対称性は<点群>で記述でき,3次元の<結晶点群>は32種類です.
(注)<結晶点群>の対称操作は周期性と両立しなければならないので,ただの点群とは異なり,
回転対称は2,3,4,6回軸に限定されます.
格子を法として(あるいは,並進群を核として)準同型写像をすると,結晶空間群の230種類を,結晶点群の32種類に還元できます.
$$\mit\Phi /T \cong G$$ , $$T \vartriangleleft \mit\Phi $$ ($$\mit\Phi $$結晶空間群,$$T $$並進群,$$G$$結晶点群)
2.双対空間.コンボリューションのFourier変換.Curieの原理(因果律)
結晶格子をFourire変換すると逆格子が得られます.結晶格子($$r-$$空間)と逆格子($$R-$$空間)は,Fourier変換で移り変わる互いに双対な空間です.結晶の電子密度関数$$ρ(r)$$とそのFourier変換F(R)は,1:1に対応し,両者の対称性は同じです.
電子密度分布$$ρ(r)$$により散乱されるX線の散乱振幅は$$F(R)$$で,$$ρ(r)$$のFourier変換にほかなりません.観測される散乱強度は$$|F(R)|^{2}$$で散乱振幅$$F(R)$$の位相情報は失われます.
$$Tr[\rho (r)]=F(R)$$, $$Tr[\rho (r)*\rho (r)]=|F(R)|^{2}$$
結晶の対称心の有無にかかわらず,観測されるX線散乱強度には,対称心が生じます:$$|F(-R)|=|F(R)|$$,これをFriedel則と言います.
Friedel則は,もっと大きい次のCurieの原理の一部です.
原因である「結晶構造の対称性」は,結果である「その結晶で生じる現象の対称性」に反映される.
(例1)結晶構造に,4回対称性が存在すれば,X線回折像の対称性に,少なくとも4回対称性は反映される.しかし,X線回折像に4回対称性が存在しても,結晶に必ずしも4回対称性が存在するわけではない.
これを回折対称の上昇という.
(例2)X線回折像に10回対称(5回対称⊗Friedel則)があったとしても,その原因たる結晶構造に5回対称性があるとは限らない.結晶構造の5回対称性は周期性(結晶の定義)と矛盾するのであり得ない.しかし,周期性を外せばあり得る.準結晶のモデルは,非周期のペンローズ・タイリングで実現できる.
3.点集合とベクトル集合.ホモメトリック
結晶構造(点集合)の対称性と,回折強度像(点集合のベクトル集合が作るスター)の対称性の関係を考察しましょう.両者の対称性では,回折強度像の対称性が高いわけで,与えられたベクトル集合から点集合を推理するのは,面倒な逆問題になる場合がある.
一般に,回折強度像の対称性から結晶構造の対称性は,一意に定まらず,同一の回折強度像を与える結晶構造が複数存在する可能性があります.これらをホモメトリック構造という.
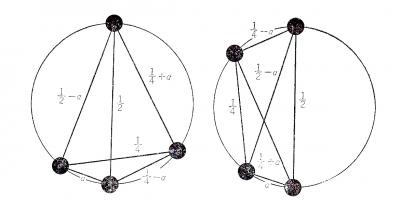
下の2つの図は,1次元のホモメトリック構造の例[Patterson(1944)].
(注)この図の見方は,1次元の単位胞が全円周(長さ1)です.図中に描き込まれた長さは円弧に沿って測ります(弦の長さではない).円周(長さ1)のどこか1点で切って,線分(長さ1)に延ばします.この線分を1次元のタイルのように並べていくと1次元の周期的な図形になります.この図形には黒い点が並んでいますが,2つの図形で黒点の配列は異なります.それにもかかわらず,出現する黒点間の間隔の種類は2つの図形で同じになります.