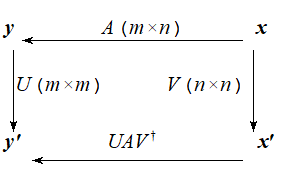■特異値分解
複素行列$$A(m \times n),m \ge n$$は,適当なユニタリー行列$$U(m \times m)$$と$$V(n \times n)$$を用いれば,
$$UAV^{ \dagger }=\mit\Sigma $$,あるいは,$$A=U^{ \dagger }\mit\Sigma V$$に分解できる.これを,Aの特異値分解という.
(ただし,$$V^{ \dagger }$$は$$V$$の共役転置行列.$$A$$が実数行列の場合は転置のみ$$V^{'}$$).
$$\mit\Sigma (m×n)=\left[ \begin{array}{@{\,} cccc @{\, } }
\sigma _{1} & & & 0 \\[0mm]
& \ddots & & \\[0mm]
& & \sigma _{r} & \\[0mm]
& & & \\[0mm]
0 & & & 0
\end{array} \right] =\left[ \begin{array}{@{\,} cc @{\, } }
\mit\Sigma _{r} & 0_{n-r} \\[0mm]
0_{m-r,r} & 0_{m-r,n-r}
\end{array} \right] , \sigma _{1} \ge \sigma _{2} \ge \cdots \ge \sigma _{r} > 0$$
ここで,$$\sigma _{1} \ge \sigma _{2} \ge \cdots \ge \sigma _{r} > 0$$を$$A$$の特異値と呼ぶ.
$$r$$は$$\textrm{rank}(A)$$に等しい.
$$AA^{ \dagger }=U^{ \dagger }\mit\Sigma VV^{ \dagger }\mit\Sigma ^{'}U=U^{ \dagger }\mit\Sigma ^{2}U$$, $$ \because \Sigma \Sigma ^{'}=\Sigma ^{2}(m×m) $$
$$AA^{ \dagger }$$の固有値は;$$\sigma _{1}^{2}, \sigma _{2}^{2}, \cdots , \sigma _{r}^{2}, 0, \cdots ,0$$(0の個数は$$m-r$$)
$$A^{ \dagger }A=V^{ \dagger }\Sigma ^{'}UU^{ \dagger }\Sigma V=V^{ \dagger }\Sigma ^{2}V$$, $$ \because \Sigma ^{'}\Sigma =\Sigma ^{2}(n×n)$$
$$A^{ \dagger }A$$の固有値は;$$\sigma _{1}^{2}, \sigma _{2}^{2}, \cdots , \sigma _{r}^{2}, 0, \cdots ,0$$(0の個数は$$n-r$$)
線形写像 $$ y=Ax (x∈C^{n},y∈C^{m})$$があり,それぞれの空間でユニタリ変換;
$$ x'=Vx$$, $$y'=Uy$$をすると,$$y'=UAV^{ \dagger }x'=\mit\Sigma x'$$にできることを述べている.
■最小2乗法
既知の実数行列$$A(m×n)$$と$$b(m×1)$$に対して,
$$||Ax-b||^{2}=(Ax-b)’(Ax-b)$$を最小にする$$x$$を求める.
特異値分解ができたら;$$UAV'=\Sigma$$,$$A=U'\Sigma V$$が成立している.
($$A$$は実行列なので,$$U,V$$は直交行列となり$$U'=U^{-1}$$などの性質がある.)
最小2乗法は,$$||\Sigma Vx-Ub||^{2}$$を最小にする$$x(n×1)$$を求める課題になる.
$$\textrm{rank}(A)=r≦n<m$$とする.$$\Sigma (m×n), V(n×n), U(m×m),x(n×1)$$の型であった.
$$r=n$$の場合を考える.
$$\mit\Sigma \equiv \left[ \begin{array}{@{\,} c @{\, } }
\mit\Sigma _{n \times n} \\[0mm]
O_{m-n \times n}
\end{array} \right] $$, $$V \equiv \left[ \begin{array}{@{\,} c @{\, } }
V_{n \times n}
\end{array} \right] $$の型であるから,
$$\mit\Sigma Vx=\left[ \begin{array}{@{\,} c @{\, } }
\mit\Sigma _{n \times n}V_{n \times n} \\[0mm]
O_{m-n \times n}
\end{array} \right] \left[ \begin{array}{@{\,} c @{\, } }
x_{1} \\[0mm]
x_{2} \\[0mm]
\vdots \\[0mm]
x_{n}
\end{array} \right] =\left[ \begin{array}{@{\,} c @{\, } }
c_{n} \\[0mm]
O_{m-n}
\end{array} \right] $$
一方,
$$Ub=\left[ \begin{array}{@{\,} c @{\, } }
a_{n} \\[0mm]
a_{m-n}
\end{array} \right] $$
従って,$$ \parallel \mit\Sigma Vx-Ub \parallel ^{2}= \parallel \left[ \begin{array}{@{\,} c @{\, } } c_{n}-a_{n} \\[0mm] -a_{m-n} \end{array} \right] \parallel ^{2} = \parallel c_{n}-a_{n} \parallel ^{2} + \parallel a_{m-n} \parallel ^{2} $$
特異値分解の結果を用いると,第1項は0になり,第2項は残差の2乗を与える,
$$ \mit\Sigma _{n \times n}V_{n \times n}\left[ \begin{array}{@{\,} c @{\, } } x_{1} \\[0mm] x_{2} \\[0mm] \vdots \\[0mm] x_{n} \end{array} \right] = \left[ \begin{array}{@{\,} c @{\, } } a_{1} \\[0mm] a_{2} \\[0mm] \vdots \\[0mm] a_{n} \end{array} \right] $$を解いて$$\left[ \begin{array}{@{\,} c @{\, } }
x_{1} \\[0mm]
x_{2} \\[0mm]
\vdots \\[0mm]
x_{n}
\end{array} \right] $$を得る.