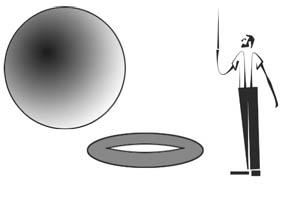
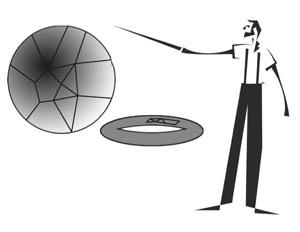
図28 左は球状の生地、右はベーグルの生地。パン屋さんは、左の生地を取り、細長い円柱になるように巻き、(トポロジーでは、充填された円柱は充填された球と区別がつかない)曲げて、この円柱の端をつなぎました。そうして球がベーグルになってしまった...。止まれ、接着は不可(許されません)! オブジェクトの種類が変更されます。
----------
私たちは、球の表面を取って曲げ、しわを寄せ、伸ばしてみましょう、どこも破らず、2つの点を1つに接着してはいけません。このようにして、例えば立方体を作ることができます。その方法を理解するために、ゴムでできた円から正方形を得る方法を示すなら、正方形の形を取るまで、円の境界の4つの点を外側に引っ張る。具体的には、円の境界の点が、正方形の外周の点に変わります。
縮めたサッカーボールのゴム表面を使って、いろいろなものを作ることができます。しかし、トポロジーが許す広い可能性の中でも、車の形表面を作るのは直感的に難しいと思います。球、楕円体、リンゴ、スイカ は作れますが、引き裂くか、いくつかの点を一緒に接着しないと、球からベーグルを作ることはできません。以上によれば、次の2つのタスクは区別する必要があります。1)膨らんだ風船から膨らんだベーグルを作る、2) 風船の表面からベーグルの表面を作る。第1の問題は、図28のキャプションで「解決」されています。
そしてオイラーは、この記述が証明できるかどうかに疑問を持った。直感的には全く問題ないのですが、数学は明白なことを厳密に証明された言語に翻訳するという問題を抱えています。結局のところ、例えば平面上に住む文明を発見したとしても、問題の事実はその住人には明らかではない(挿話2を参照)。そして、数学の力を借りて、定理の内容を伝えることができるようになります。
---------
(挿話2)アインシュタインのトポロジー
かつてA.アインシュタインは、彼の発見の本質は何かを誰にでもわかりやすい言葉で、非常に簡潔に説明するように求められました。彼は答えた:私たちは皆、目隠しされた小さな虫のように、大きな球の表面を這っています。私は、自分の住んでいる世界が曲がっていることに初めて気がつきました。しかし、具体的にどのように湾曲しているのか(空間のトポロジカルなタイプが何であるか)はまだよくわかっていません。
ーーーー
そして、ここからが本題です。数年前に数学者のG.ペレルマンが同様の事実を立証しましたが、大次元空間でのみです。局所的に湾曲した3次元空間に似ている多次元空間の図形についての事実。私たちは3次元空間に住んでいて、4次元を見たり感じたりすることはできません。第4次元が時間であることを推論することしかできないが、目では把握できない。だから、大次元空間の球体からトーラスを作ることは不可能だと冷静に納得することはできません。(結局のところ、4次元空間では、上述のように、トポロジーのルールを守りながら、左側に心臓のある人を右側に心臓のある人に変えることは可能である)
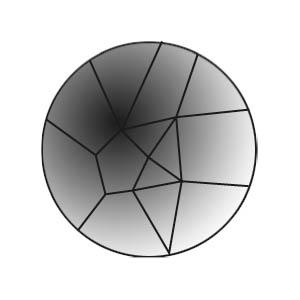
それを証明できる言語が必要です。そして、ペレルマンが「ポアンカレ仮説」を証明するまでに何年もかかった(証明された後は、ポアンカレ仮説やポアンカレ-ペレルマンではなく、ペレルマン定理と呼ばれるようになった)。オイラーが始めた分野は大きくなった。彼は、皆が明白だと思うことを正確で鉄壁の数学的推論に翻訳しました。球、スイカ、地球、湾曲した多面体、どんな丸いものでも表面に何かしらの地図を描いた(図29)。
トポロジーの観点から言えば、どんな多面体も球体である。4面体は球体、立方体は球体、8面体、どんな平行6面体もすべて球体です。例えば、ゴムで作って膨らませばサッカーボール、つまり球体になる。オイラーの仕事以前には、トポロジーそのものが存在しませんでした。
オイラーは、これらの物体がすべて同じであると直感した。具体的にはどのような形でどう説明するのか?彼は、球体の表面とベーグルの表面とプレッツェルの表面が同じではないことをどうやって証明するかという問題に特に興味を持っていた。
最初の質問に対する答えは、後にアンリ・ポアンカレによって明らかにされた(オーギュスト・コーシーが「連続関数」とは何かを明確にした後)。
オイラーはすぐに第2の問題(2つの面の非一様性の証明について)に目を向け、これを見事に解いた。
ーーーーーーーーーー
オイラー標数:(頂点の数)-(辺の数)+(面の数)
球体上に描いた地図とトーラス(ベーグル表面)に描いた地図で、オイラー標数を数えると違いがあり,この特性はトポロジー的な連続変形で変化するはずはないのだから,トポロジー的に違うものでなければなりません.
オイラー標数は:2(球表面),0(トーラス)
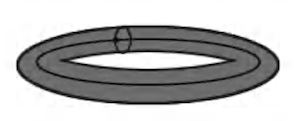
頂点の数1,辺の数2,面の数1