3次元空間(幾何学的空間)の対称群 $$G$$ の一般化は,A.V.シュブニコフの”反対称的に等価”という概念から始まりました.結晶(幾何学的)空間で定義した”対称的に等価”という概念[鏡映対称,回転対称,あるいは(平行移動)並進などで重なる]は,幾何学的空間で行われる対称操作を定義し,それらの対称操作の作る群(点群や空間群)として,空間の対称性が記述できました.シュブニコフの考えた”反対称的に等価”という概念は,幾何学的な空間とは別の次元の空間で行われる対称操作を導きます.空間の位置は動かさず,空間の点の特性(例えば,色)を,塗り変える操作をイメージしてください.黒⇔白,+⇔-,などの2値の特性の変換が”反対称的に等価”の例です.幾何空間での変換と特性空間(代表して色空間と呼ぶ)での変換とを結合した一般化された変換は,反対称群(黒-白群,あるいは,シュブニコフ群)という従来の点群や空間群を拡張した新しい対称群を生み出します.
このような反対称(黒-白)群は,群の拡大という数学理論で興味深いだけでなく,その結晶構造で観測される特性の対称性記述に有用です.
◆
磁性体の磁力は,その結晶構造中の鉄などの磁性の原子やイオンが所有する磁気モーメント(その原子に束縛されている電子の自転-スピン-で,スピンベクトルは上向-下向の2値をとります)の総和です.結晶構造中の磁性原子の位置に,スピンの向きの矢印を書き込んだ図の例をご覧ください.
一般に,原子の磁気モーメントは,各原子に束縛されている電子の軌道角運動量とスピン角運動量の総和ですが,外殻に3d電子をもつ遷移金属 Ti, V, Cr, Mn, Fe, Co, Niでは,スピン角運動量で磁気モーメントが決まります.
ただし,正確に言うと,3d電子がそれぞれの原子に(局在)束縛されているのは,酸化物,Fe2O3,NiOなどでの話で,Fe, Coなどの金属結合状態にあるCo, Feなどでは,3d電子はブロッホ関数で記述される周期的な電子雲となり結晶全体に広がり,エネルギー・バンドを形成します.上向きスピンと下向きスピンが占有する状態密度の差だけのスピン角運動量が残ります.
磁性の予備知識はここまでにして,主題の反対称群に話を戻します.
結晶構造の原子の位置は,3次元幾何空間(結晶空間)の座標で指定でき,結晶構造の対称性は従来の空間群で記述できます.しかし,結晶構造中の磁性原子の電子スピンの反転対称操作は,幾何学空間とは別次元の”特性(色)空間”で行われるものです.強磁性体の特性を記述する対称操作は,幾何世界の対称操作に,スピン空間での対称操作を結合した”一般化された対称操作”で,これらの結合された対称操作の作る群が反対称群です.
特性の2値は;スピンの↓・↑,電荷の+・ー,など;色々なものがありますが,特性を代表して「色」と呼ぶことにし,特性が2値のものは,反対称群(黒-白群,シュブニコフ群)になります.
可能な特性値を多値$$p>2$$の空間に拡張すれば,それらは,p-色の色付群,あるいは,ベーロフ群と呼ばれるものになります.幾何学的空間の点の配置に関する限り,従来の対称群(点群や空間群)で記述されますが,それらの点を$$p$$色に塗り分けたものの対称性の記述は,このベーロフ群を用います.
$$p$$-色で塗分けるといっても,適当に塗るのではなく対称操作に従って塗分けるのですから,同じ色について同数ずつあるはずです.そして,p色の色置換は,幾何学的空間の変換と結びついているので,$$p$$の数は空間の対称操作の位数と矛盾しない数値に限定されます.
◆
ここでは,まず,黒-白群(2色の色付群)の作り方を説明します:
黒-白群$$G'$$で記述される黒と白の点で構成された構造が与えられたとします.①もし,色が判別できない眼鏡を通して見たとすれば,これらの点は皆同じ色ですから,普通の幾何空間での対称群Gで記述できるはずです.ゆえに,当然,$$G’$$と$$G$$は同型な群です: $$G’≅G$$ .
②この構造中の黒,白の点は,色反転操作で互いに入れ替わらなければならないので,同数ずつあります.従って,群$$G’$$は次のように剰余類展開できます.
$$ G^{*} $$は,$$G$$の指数2の部分群で,同色の点を変換する(色を変えない変換よりなる)部分群.$$g'$$は位数2の色の塗り替えを伴う変換操作です.
$$G’$$の剰余類展開
$$
G'=G^{*}\cup G^{*}g' , G^{*}⊂G
$$
反対称群$$G’$$は,同型な古典群(従来の群)$$G$$と $$G^{*}$$
を用いて,2項記号 $$G/G^{*}$$ と標記されます.
$$G’$$の剰余類展開の式で,第1項は対称演算の集合の作る群,第2項は反対称演算の作る群で,両者の合併集合として反対称群$$G’$$が表現されています.
古典的な3次元結晶空間群230種類は,点群と並進群を掛け合わせて「並進群を点群で拡大して」得られます.反対称群も同様ですが,反対称要素が点群の方にあるために得られる反対称群は674種類,並進の方に反並進があるために得られる反対称群は517種類であることが知られています.
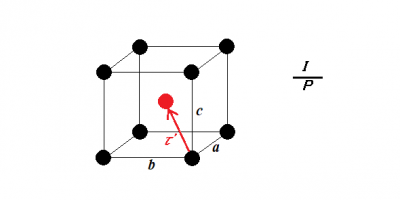
表紙の図は,簡単な反対称の例で,体心格子 I の格子点のうち同一色の格子点は単純格子 $$P$$ ですので,これを反対称群の2項記号で標記すると$$I/P$$
となります.この反対称群の格子点を定義するベクトルは$${a, b, c, \tau’}$$で,$$\tau=(a+b+c)/2$$.$$\tau$$は,体心の位置を指定するベクトルです.’がついている意味は,これが色を反転する並進操作であることを示しています.この簡単な反対称群は反並進が起因で生じた群です.
反対称群(シュブニコフ群)やp-色の色付き群(ベーロフ群)は,3次元の空間次元+1次元の特性空間で定義されますが,
特性空間も3次元空間と等価な場合の4次元空間群の特殊な一部と見做すこともできます.