230の結晶空間群を数え上げた一人にフェドロフがいます.フェドロフはどのようにして空間群の数え上げを行ったのでしょうか.
注)
230種の3次元の結晶空間群の数え上げの研究は,フェドロフ(露,ぺテルスブルグ大,鉱物学教授),シェンフリーズ(独,フランクフルト大,数学教授),バーロウ(英,ロンドンの実業家)により,1890-1895の間に,それぞれ互いに独立に完成しました.フェドロフの結果が完璧であったことは,3者の認めるところであり,3次元結晶空間群はフェドロフ群とも呼ばれています.
3次元の結晶空間を対象とする前に,2次元の結晶空間を対象にして,結晶空間(=離散的な周期空間,デジタル化された空間)の構造を記述する群論を十分に理解するのが良いと思います.それは,3次元やそれ以上の高次元にも対応できる応用力となります.
2次元の結晶空間で,同一の平行多辺形タイルで平面をタイル張りする(重なりもなく隙間もない)ことが,この課題のスタートとなります.
次に,1つのタイルを同価な部分に分割します.この分割は,タイルの対称性を使って,そのタイルの非対称要素と言われる同価部分に分割します.
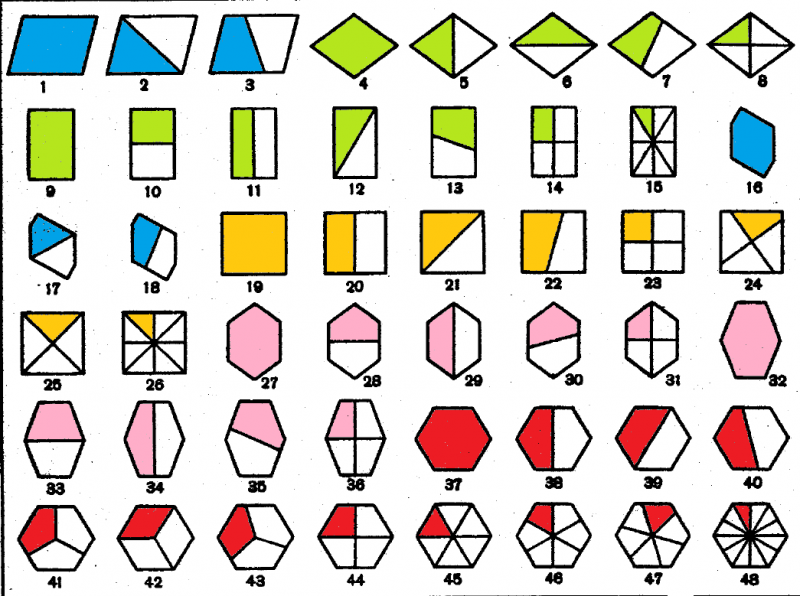
1つのタイルを分割できる同価部分の数は,タイルの点群の位数に等しい数です.こうして分割された部分の形には対称性がなく,非対称要素と呼ばれます.表紙に掲載した平面のタイル張りができる8つの平行多辺形から出発します.
平行多辺形の同価部分への分割方法
これら80種類のタイルは,それぞれ,並進だけで平面を張り詰めることのできる平行多辺形です.着色した部分はそれぞれの平行多辺形の非対称部分で,1つの例外(15番)を除いて,そのタイルの点群の対称操作を非対称部分に作用させ,そのタイルの全体を作ることができます.
このタイル張りで生じる平面群は$$p2 \tilde{a}\tilde{b} $$
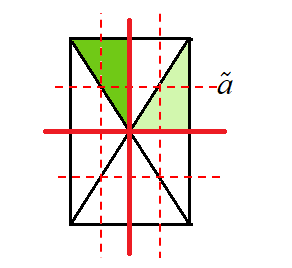
15番のタイルの場合には,濃い黄緑色に着色した非対称要素に,タイルの点群$$2mm$$の対称操作を作用させても,薄い黄緑色に着色した部分へ移動し重ねることができません.この移動には映進操作$$\tilde{a}$$が必要です.
今,タイルの並進で無限に広い2次元平面を張り詰めるので,映進操作も対称操作に含めることができます.
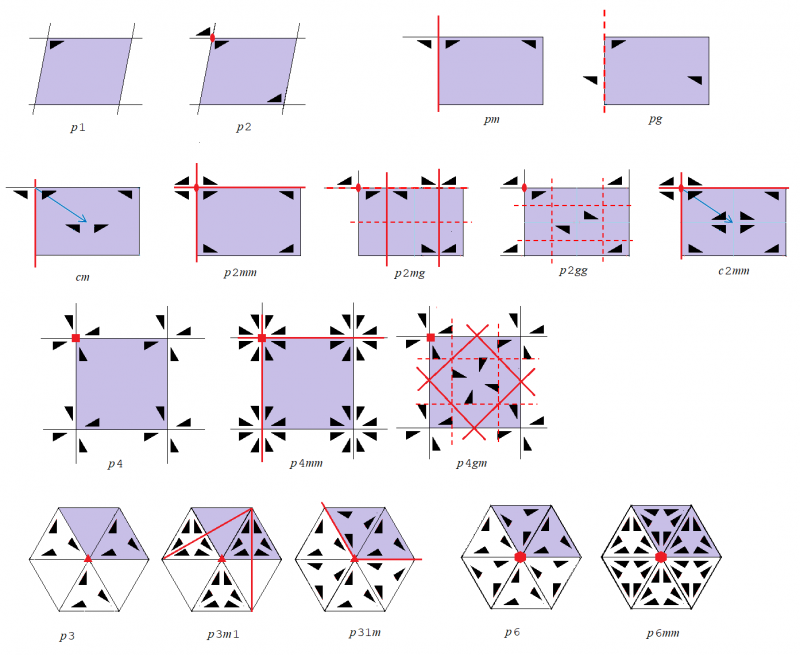
これらの図形の点群を調べると,点群が重複しているものがたくさんあります.全部で17種類の平面群に整理することができます.
注)15番のタイル張りは,以下の$$p2gg$$⑧に対応.
⇒3次元結晶空間への発展を見る